| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
mathadores
Maître
 Nombre de messages : 107 Nombre de messages : 107
Age : 29
Localisation : Kénitra
Date d'inscription : 28/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 16 Mar 2011, 12:20 Mer 16 Mar 2011, 12:20 | |
| je crois que j'ai vu l'exo dans une autre place .
il te manque un petit truc dans l'enoncé c'est que dans l'autre exo il y'a x<y alors
la solution est -√2 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 16 Mar 2011, 16:21 Mer 16 Mar 2011, 16:21 | |
| - boubou math a écrit:
- EXO 77
Soit A ET B de point differante du plan
Trouvez tous les point M tels que MA/MB=k (j'ai une solution mais je suis po sur) Voici ma solution, comme je vous ai promi le lundi: On a: ^2-(k.\overrightarrow{MB})^2=0 \\&\Leftrightarrow (\overrightarrow{MA}-k.\overrightarrow{MB})(\overrightarrow{MA}+k.\overrightarrow{MB})=0\end{align*}) . Soit maintenant deux points 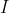 et 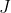 , tels que 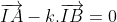 et 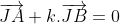 . En appliquant chasles dans la dernière relation trouvée, on trouve: (\overrightarrow{MA}+k.\overrightarrow{MB})=0&\Leftrightarrow (\overrightarrow{MI}+\overrightarrow{IA}-k.\overrightarrow{MI}-k.\overrightarrow{IB})(\overrightarrow{MJ}+\overrightarrow{JA}+k.\overrightarrow{MJ}+k.\overrightarrow{JB})=0\\&\Leftrightarrow (\overrightarrow{MI}-k.\overrightarrow{MI})(\overrightarrow{MJ}+k.\overrightarrow{MJ})=0\\&\Leftrightarrow (1-k).\overrightarrow{MI}.(1+k).\overrightarrow{MJ}=0\\&\Leftrightarrow 1-k=0\text{ ou }\overrightarrow{MI}.\overrightarrow{MJ}=0\end{align*}) . (car k+1 doit être strictement positif et non nul). *Cas premier: k=1. On trouve donc que MA=MB. Ce qui veut bien dire que l'ensemble des points M vérifiant la relation est la mediatrice du segment [AB]. *Cas second: k#1. Ainsi, selon ce qui précède, on trouve que 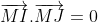 . Ce qui veut bien dire que l'ensemble des points M vérifiant la relation est le cercle dont le diamètre est [IJ]. Sauf erreur. P.S: Les résultats présents ici sont appris au tronc commun. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 16 Mar 2011, 18:18 Mer 16 Mar 2011, 18:18 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 16 Mar 2011, 18:54 Mer 16 Mar 2011, 18:54 | |
| - yasserito a écrit:
- je crois que c'est la meme solution que Mehdi.o car le probleme ici n'est pas vraiment sur la barycentre mais comme meme que si
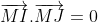 ,alors on a la solution est un cercle!! qu'est en fait qqch de la premiere annee pas de tronc commun .Au moins c'est ce que je pense ,alors on a la solution est un cercle!! qu'est en fait qqch de la premiere annee pas de tronc commun .Au moins c'est ce que je pense
amicalement  Si ma mémoire est bonne, cela fait partie du programme du tronc commun. (Le chapitre du produit scalaire). | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 16 Mar 2011, 19:09 Mer 16 Mar 2011, 19:09 | |
| - nmo a écrit:
- yasserito a écrit:
- je crois que c'est la meme solution que Mehdi.o car le probleme ici n'est pas vraiment sur la barycentre mais comme meme que si
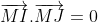 ,alors on a la solution est un cercle!! qu'est en fait qqch de la premiere annee pas de tronc commun .Au moins c'est ce que je pense ,alors on a la solution est un cercle!! qu'est en fait qqch de la premiere annee pas de tronc commun .Au moins c'est ce que je pense
amicalement  Si ma mémoire est bonne, cela fait partie du programme du tronc commun.
(Le chapitre du produit scalaire). je ne sais pas,ma memoire n'est pas trop bonne mais apres tout on peut le trouver en disant que (MI) est perpendiculaire a (MJ) alors MIJ est un triangle rectangle alors son cercle inscrit et qui contient tous les M et de centre O milieu de [IJ] et de rayon IJ/2. C.Q.D.C.Q.F.D merci pour l'eclaircissement ! | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 16 Mar 2011, 19:12 Mer 16 Mar 2011, 19:12 | |
| ca fait partie du programme TC , d'ailleur je l'ai prit d'un livre de tc (j'avais pander a un truc pareil mais je me suis bloqué f l'etape chale ) Grand merci pr la solution  | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 18 Mar 2011, 17:00 Ven 18 Mar 2011, 17:00 | |
| exercice 84 soit a,b et c des réels positifes tel que abc=1 M.Q }+\frac{1}{b^3(a+c)}+\frac{1}{c^3(a+b)}\geq&space;\frac{3}{2}) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 18 Mar 2011, 18:14 Ven 18 Mar 2011, 18:14 | |
| Solution du problème 84 :Posons : 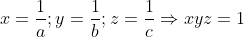 L'inégalité est équivalente à :  Or d'après C.S : .\sum&space;\frac{x^{2}}{y+z}\geq&space;(\sum&space;x)^{2}\Leftrightarrow&space;\sum&space;\frac{x^{2}}{y+z}\geq&space;\frac{\sum&space;x}{2}\geq&space;\frac{3}{2}) Selon I.AG. CQFD | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 19 Mar 2011, 20:23 Sam 19 Mar 2011, 20:23 | |
| 84 jai pas compri la derniere ligne stp tu peu un pti peu simplifier jai resolu le problem mai avec une autre teknik regarde
apre avoir suggerer que x=1/a y=1/b z=1/c
x^2/(y+z) >= x/(y+z)
y^2/(x+z) >=y/(x+z)
z^2/(x+y) >=z/(x+y)
ET
dapre chevy chev x/(y+z) +y/(x+z)+z/(x+y) >=1/3(x+y+z)(1/(y+z) + 1/(x+z) +1/x+y) )
donc x/(y+z) +y/(x+z)+z/(x+y) >= 1 +1/3 (x/(y+z) +y/(x+z)+z/(x+y))
donc x/(y+z) +y/(x+z)+z/(x+y)>= 3/2 | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 19 Mar 2011, 20:30 Sam 19 Mar 2011, 20:30 | |
| - amigo-6 a écrit:
- 84 jai pas compri la derniere ligne stp tu peu un pti peu simplifier jai resolu le problem mai avec une autre teknik regarde
apre avoir suggerer que x=1/a y=1/b z=1/c
x^2/(y+z) >= x/(y+z)
y^2/(x+z) >=y/(x+z)
z^2/(x+y) >=z/(x+y)
ET
dapre chevy chev x/(y+z) +y/(x+z)+z/(x+y) >=1/3(x+y+z)(1/(y+z) + 1/(x+z) +1/x+y) )
donc x/(y+z) +y/(x+z)+z/(x+y) >= 1 +1/3 (x/(y+z) +y/(x+z)+z/(x+y))
donc x/(y+z) +y/(x+z)+z/(x+y)>= 3/2 qui vous a di que x et y et z sont postérieures de 1 ou a et b et c sont inférieures de 1? | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 19 Mar 2011, 20:47 Sam 19 Mar 2011, 20:47 | |
| Hey les gars, c'est dans quel logiciel que vous pouvez écrire ces formules mathématiques? Parce je suis nouveau ici et je sais pas quoi faire!  | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 19 Mar 2011, 20:57 Sam 19 Mar 2011, 20:57 | |
| - konica a écrit:
- Hey les gars, c'est dans quel logiciel que vous pouvez écrire ces formules mathématiques? Parce je suis nouveau ici et je sais pas quoi faire!
 Salut, Tu les trouveras dans ce lien http://www.codecogs.com/latex/eqneditor.php  | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 19 Mar 2011, 22:43 Sam 19 Mar 2011, 22:43 | |
| qui vs a di que x et y et z sont posterieur a 1
bin
a et b et c son des nombre positifs reel
donc x>0 alors x^2 >=x n'est ca pas lol | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 19 Mar 2011, 22:54 Sam 19 Mar 2011, 22:54 | |
| - amigo-6 a écrit:
- qui vs a di que x et y et z sont posterieur a 1
bin
a et b et c son des nombre positifs reel
donc x>0 alors x^2 >=x n'est ca pas lol juste amicalement prenez x=1/2>0 est ce que (1/2)²>1/2 est ce que 1/4>1/2 est ce que 2>4? je ne crois pas peut etre c'est de ma faute j'avais une base mediocre mais au total je crois que x doit etre posterieur a 1 pour que x² soit posterieur de x! amicalement  | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 20 Mar 2011, 18:26 Dim 20 Mar 2011, 18:26 | |
| | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 20 Mar 2011, 20:03 Dim 20 Mar 2011, 20:03 | |
| J'aime ta facon de parler mon ami | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 10:10 Lun 21 Mar 2011, 10:10 | |
| Azery 1995, merci beaucoup!!  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 13:18 Lun 21 Mar 2011, 13:18 | |
| EXO 84
a,b,c>=0 et abc=1
montrez que (a-1+1/b)(b-1+1/c)(c-1+1/a)=<1 | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 13:33 Lun 21 Mar 2011, 13:33 | |
| Voilà mon exercice: Soit x,y et z trois nombres appartenant à IR, montre que: 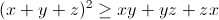 | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 14:24 Lun 21 Mar 2011, 14:24 | |
| salam
x²+y²=>-2xy
x²+z²=>-2xz
z²+y²=>-2yz
2(x²+y²+z²)=>-2(xy+yz+xz)
x²+y²+z²+xy+yz+xz=>0
(x+y+z)²=>xy+yz+zx | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 18:26 Lun 21 Mar 2011, 18:26 | |
| Hmmmm! Non!
Au début c'est:
x²+y²=>2xy
x²+z²=>2xz
z²+y²=>2yz
2(x²+y²+z²)=>2(xy+yz+xz)
Alors:
x²+y²+z²=>xy+yz+zx
Et bravo! | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 18:37 Lun 21 Mar 2011, 18:37 | |
| konica
x²+y²+z² est différant de (x+y+z)²
amicalement
Dernière édition par boubou math le Jeu 03 Nov 2011, 18:47, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 20:05 Lun 21 Mar 2011, 20:05 | |
| x² + y² >= -2xy c'est pas toujours juste . x = 2 et y = -2 => 4 >= 8 (!!!!!) | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 20:23 Lun 21 Mar 2011, 20:23 | |
| Az360 Amicalement  je crois que a^2+b^2 >= -2ab est toujours juste quand tu pren a=2 et b =-2 a^2+b^2= 8 et-2ab=8 donc on peu dire a^2+b^2 >= -2ab amicalement^^ | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 20:36 Lun 21 Mar 2011, 20:36 | |
| Je crois que c'est toujours juste puisque pour tout x,y de IR : (x+y)²>=0 soit x²+y²+2xy>=0 soit x²+y²>=-2xy Dans ton contre-exemple, je pense que t'as fait une faute de calcul pour x=2 et y=-2 x²+y²=2²+(-2)²=4+4=8 >= -2xy=(-2)*(-2)*2=8 AMICALEMENT,  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
