| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 20 Mar 2011, 20:03 Dim 20 Mar 2011, 20:03 | |
| J'aime ta facon de parler mon ami | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 10:10 Lun 21 Mar 2011, 10:10 | |
| Azery 1995, merci beaucoup!!  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 13:18 Lun 21 Mar 2011, 13:18 | |
| EXO 84
a,b,c>=0 et abc=1
montrez que (a-1+1/b)(b-1+1/c)(c-1+1/a)=<1 | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 13:33 Lun 21 Mar 2011, 13:33 | |
| Voilà mon exercice: Soit x,y et z trois nombres appartenant à IR, montre que: 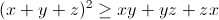 | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 14:24 Lun 21 Mar 2011, 14:24 | |
| salam
x²+y²=>-2xy
x²+z²=>-2xz
z²+y²=>-2yz
2(x²+y²+z²)=>-2(xy+yz+xz)
x²+y²+z²+xy+yz+xz=>0
(x+y+z)²=>xy+yz+zx | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 18:26 Lun 21 Mar 2011, 18:26 | |
| Hmmmm! Non!
Au début c'est:
x²+y²=>2xy
x²+z²=>2xz
z²+y²=>2yz
2(x²+y²+z²)=>2(xy+yz+xz)
Alors:
x²+y²+z²=>xy+yz+zx
Et bravo! | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 18:37 Lun 21 Mar 2011, 18:37 | |
| konica
x²+y²+z² est différant de (x+y+z)²
amicalement
Dernière édition par boubou math le Jeu 03 Nov 2011, 18:47, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 20:05 Lun 21 Mar 2011, 20:05 | |
| x² + y² >= -2xy c'est pas toujours juste . x = 2 et y = -2 => 4 >= 8 (!!!!!) | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 20:23 Lun 21 Mar 2011, 20:23 | |
| Az360 Amicalement  je crois que a^2+b^2 >= -2ab est toujours juste quand tu pren a=2 et b =-2 a^2+b^2= 8 et-2ab=8 donc on peu dire a^2+b^2 >= -2ab amicalement^^ | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 20:36 Lun 21 Mar 2011, 20:36 | |
| Je crois que c'est toujours juste puisque pour tout x,y de IR : (x+y)²>=0 soit x²+y²+2xy>=0 soit x²+y²>=-2xy Dans ton contre-exemple, je pense que t'as fait une faute de calcul pour x=2 et y=-2 x²+y²=2²+(-2)²=4+4=8 >= -2xy=(-2)*(-2)*2=8 AMICALEMENT,  | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 21 Mar 2011, 20:37 Lun 21 Mar 2011, 20:37 | |
| Désolé, Mr amigo-6. J'avais pas vu ton message.
| |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 08:22 Mar 22 Mar 2011, 08:22 | |
| OUi Vous avez raison .  | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 12:43 Mar 22 Mar 2011, 12:43 | |
| à Boubou maths! Désolé, c'est une faute, je sais pas ce que je fais, désoléencore une fois! Alors je vais commencer! On doit montrer que (x+y+z)²=>xy+yz+zx Je vais commencer! (x+y+z)²=x²+y²+z²+2(xy+yz+zx) D'où: (x+y+z)²=>xy+yz+zx x²+y²+z²+2(xy+yz+zx)=>xy+yz+zx x²+y²+z²+xy+yz+zx=>0 Alors si on veut montrer que (x+y+z)²=>xy+yz+zx, ça suffit de montrer que x²+y²+z²+xy+yz+zx=>0. Ben, je vais commencer: x²+y²=>-2xy y²+z²=-2yz z²+x²=-2zx Alors: 2x²+2y²+2z²=>-2xy-2yz-2zx 2(x²+y²+z²)=>-2(xy+yz+zx) x²+y²+z²=>-(xy+yz+zx) x²+y²+z²+xy+yz+zx=>0 Et enfin: (x+y+z)²=>xy+yz+zx Salutations et désolé encore une fois!  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 12:49 Mar 22 Mar 2011, 12:49 | |
| - Spoiler:
à Boubou maths!
Désolé, c'est une faute, je sais pas ce que je fais, désoléencore une fois!
Alors je vais commencer!
On doit montrer que (x+y+z)²=>xy+yz+zx
Je vais commencer!
(x+y+z)²=x²+y²+z²+2(xy+yz+zx)
D'où: (x+y+z)²=>xy+yz+zx
x²+y²+z²+2(xy+yz+zx)=>xy+yz+zx
x²+y²+z²+xy+yz+zx=>0
Alors si on veut montrer que (x+y+z)²=>xy+yz+zx, ça suffit de montrer que x²+y²+z²+xy+yz+zx=>0.
Ben, je vais commencer:
x²+y²=>-2xy
y²+z²=-2yz
z²+x²=-2zx
Alors: 2x²+2y²+2z²=>-2xy-2yz-2zx
2(x²+y²+z²)=>-2(xy+yz+zx)
x²+y²+z²=>-(xy+yz+zx)
x²+y²+z²+xy+yz+zx=>0
Et enfin:
(x+y+z)²=>xy+yz+zx
Salutations et désolé encore une fois!
c'est qui est en rouge est faux ,sinon l'idée est bonne (c'est ce qu'a fait Mr abdelkrim-amine) | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 12:51 Mar 22 Mar 2011, 12:51 | |
| Je rappelle l'exo non résolu exo: EXO 84
je poste la réponse ver 18:00 | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 18:19 Mar 22 Mar 2011, 18:19 | |
| jai solution 84 att stp jlecri | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 18:29 Mar 22 Mar 2011, 18:29 | |
| bon 84)
(a-1+1/b) (b-1+1/c) (c-1+1/a)= abc(1-bc+c)(1-ac+a)(1-ab+b)
=(1-bc+c)(1-ac+a)(1-ab+b)
on pren (1-bc+c)(1-ac+a)=x et (1-ac+a)(1-ab+b)=y et (1-bc+c)(1-ab+b)=z
x=(1-bc+c)(1-ac+a)
=2c+a-bc-ac^2
=2c+a-bc-c/b
=2c+a-c(b+1\b)
b+1/b>2 ( on peu le demontrer si vs ne savais pas jpeu vs la demontrer)
donc -c(b+1\b)<=-2c
x<a
DE la meme methode on demontre que y<b et z<c donc
xyz<abc donc (a-1+1/b)^2 (b-1+1/c)^2 (c-1+1/a)^2< 1
donc (a-1+1/b) (b-1+1/c) (c-1+1/a) <1
| |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 18:54 Mar 22 Mar 2011, 18:54 | |
| Trés bien Amigo-6
je poste une autre solution
posant a=x/y b=y/z c=z/x
l'inegalité devient (x/y-1+z/y)(y/z-1+x/z)(z/x-1+yx)=[(x+y-z)(x-y+z)(-x+y+z)]/xyz
maintenant il faut prouver que (x+y-z)(x-y+z)(-x+y+z)=<xyz
on pose x=a+b-c et y=a-b+c et z=-a+c+b ainsi on a x+y=2a et y+z=2c et z+x=2b
on a x+y>=2Vxy
et y+z>=2Vyz ainsi on a (x+y)(y+z)(z+x)>=8xyz
et x+z>=2Vxz
on remplace par a et b et c et on obtient abc>=(a+b-c)(a-b+c)(-a+b+c)
d'ou (a-1+1/b) (b-1+1/c) (c-1+1/a)=<xyz/xyz=1 ( les a ,b ,c dans la demonstration de (x+y-z)(x-y+z)(-x+y+z)=<xyz sont differant des premier )AMICALEMENT
| |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 19:04 Mar 22 Mar 2011, 19:04 | |
| ui c'est juste mais je pense que ta un petit peu compliqué les choses^^ mai ca reste une bonne méthode .amicalement | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 19:05 Mar 22 Mar 2011, 19:05 | |
| ca m'a etais facile pcq je savais deja l'inegalité (x+y-z)(x-y+z)(-x+y+z)=<xyz
| |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 19:07 Mar 22 Mar 2011, 19:07 | |
| EXO 85
Prouver que si cos(x)+sin(x)<0 alors cos^1991(x)+sin^1991(x)<0 | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 22 Mar 2011, 20:35 Mar 22 Mar 2011, 20:35 | |
| - amigo-6 a écrit:
- bon 84)
(a-1+1/b) (b-1+1/c) (c-1+1/a)= abc(1-bc+c)(1-ac+a)(1-ab+b)
=(1-bc+c)(1-ac+a)(1-ab+b)
on pren (1-bc+c)(1-ac+a)=x et (1-ac+a)(1-ab+b)=y et (1-bc+c)(1-ab+b)=z
x=(1-bc+c)(1-ac+a)
=2c+a-bc-ac^2
=2c+a-bc-c/b
=2c+a-c(b+1\b)
b+1/b>2 ( on peu le demontrer si vs ne savais pas jpeu vs la demontrer)
donc -c(b+1\b)<=-2c
x<a
DE la meme methode on demontre que y<b et z<c donc
xyz<abc donc (a-1+1/b)^2 (b-1+1/c)^2 (c-1+1/a)^2< 1
donc (a-1+1/b) (b-1+1/c) (c-1+1/a) <1
Cela est faux, vu que vous devez démontrez que les ombre x,y,z sont strictement positifs sinon vous ne pouvez pas multiplier les côtés. Sinon cela est facile à prouver par disjonction des cas sur a,b,c resptecivement. P.S: Ce problème que tu as posté est un problème d'IMO, qui dépasse largement le niveau du tronc commun. Alors à quoi de poser des problèmes alors qu'on sait la solution qui figure à Animath, ou en d'autres sites ... et de se vanter, et ne me dites pas que c'est votre solution  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 23 Mar 2011, 12:32 Mer 23 Mar 2011, 12:32 | |
| j'ai pris cet exo d'une serie olympiade fait pr les TCéans et la solution que j'ai fait est la mienne voila le lien  http://arabmaths.kegtux.org/maths08/olymp/od.pdf exo 57 (pr la premiere remarque t'as raison ) | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 23 Mar 2011, 21:09 Mer 23 Mar 2011, 21:09 | |
| EXO 84
On a : cos(x) + sin(x) < 0
Donc un des deux est nécessairement strictement négatif.
Raisonnons par disjonction des cas:
1) cos(x)< 0
cos(x) + sin(x) < 0
sin(x) < -cos(x)
-sin(x)/cos(x) < 1
Comme la fonction x -> x^1991 est croissante sur IR
Alors : -sin^1991(x)/cos^1991(x) <1
sin(x)^1991(x) < -cos^1991(x)
sin^1991(x)+cos^1991(x) < 0
2) sin(x) < 0
cos(x) + sin(x) < 0
cos(x) < -sin(x)
-cos(x)/sin(x) < 1
Comme la fonction x -> x^1991 est croissante sur IR
Alors : -cos^1991(x)/sin^1991(x) <1
cos(x)^1991(x) < -sin^1991(x)
sin^1991(x)+sin^1991(x) < 0
CQFD | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 24 Mar 2011, 07:18 Jeu 24 Mar 2011, 07:18 | |
| on a pas encore etudier les fonction mais je pense que x-->x^1991 n'est po croissante sur [0,1] | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
