| | Préparation TSM:: L-1/Limites et continuité:p/Exercices. |  |
|
+11j'aime maths Othmaann ali-mes Hamouda manazerty princessdesmaths Mim mr.mertasayeker kaj mima Yassino expert_run 15 participants |
|
| Auteur | Message |
|---|
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Mar 26 Juil 2011, 13:10 Mar 26 Juil 2011, 13:10 | |
| Ok je vais envoyer 3 exercice en même temps. | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Mar 26 Juil 2011, 15:01 Mar 26 Juil 2011, 15:01 | |
| On attends toujours !  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Mar 26 Juil 2011, 15:13 Mar 26 Juil 2011, 15:13 | |
| Exercice2:Soit a un réel et  la fonction numérique définie par: 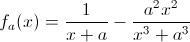 1-Déterminer l'ensemble de définition de  . 2-Déterminer les valeurs de a pour que  admet une limite en -a. Exercice3:Soient m un réel et f le fonction numérique définie par:  1-Déterminer l’ensemble de définition de la fonction f . 2-Étudier les limites de f aux bornes de l'ensemble de définition selon les valeurs de m. | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Mar 26 Juil 2011, 18:17 Mar 26 Juil 2011, 18:17 | |
| Exercice 2: - expert_run a écrit:
- Exercice2:
Soit a un réel et  la fonction numérique définie par: la fonction numérique définie par:
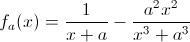
1-Déterminer l'ensemble de définition de  . .
2-Déterminer les valeurs de a pour que  admet une limite en -a. admet une limite en -a. 1)-Df={x £ IR/x+a =/= 0 et x^3 + a^3 =/= 0} Df= IR-{-a} 2)-On doit trouver les valeurs de a pour que f(x) admette une limite finie en -a : f(x) = 1/(x+a) - (x²a²)/(x^3+a^3) = (x²-ax+a² -x²a²)/(x^3+a^3) on a lim x^3 + a^3 quand x tend vers -a = 0 donc pour que f(x) admette une limite finie vers -a il nous faut simplifier par (x+a), et donc lim x²-ax+a²-a²x² doit etre =0 pour -a x²-ax+a²-a²x² = 0 <=> a² +a²+a² - a^4 = 0 <=> 3a² = a^4 <=> a = V3 ou a = -V3 ou a = 0 . pour le cas de a = 0 on aura lim 1/x = +/- oo donc ce n'est pas une solution valable. pour le cas de a=V3 : ( et donc -a = -V3 hein ! ) f(x) = ( x² -V3x + 3-3x²)/(x+V3)(x²+3-V3 x) Lima- ( -2x²-V3x + 3)/(x+V3)(x²+3-V3 x) Lima- ( x+V3)(-2x+V3)/(x+V3)(x²+3-V3x) Lima- (-2x+V3)/(x²+3-V3x) =V3/3 pour le cas de a=-V3 ( et donc -a=V3) f(x) = (x²+3+V3x-3x²)/(x-V3)(x²+3+V3x) Lima- ( x-V3)(-2x-V3)/(x-V3)(x²+3+V3x) =-V3 donc les valeurs de a sont : V3 et -V3 Exercice 3 : 1)- Df = { x £ IR / x(x-2)(x-3) =/= 0 } c'est à dire : x=/= 0 ; x =/= 2 ; x=/= 3 Df = ]-oo;0[U]0;2[U]2;3[U]3;+oo[ 2)- Etudions les limites de f(x) aux bornes de Df : *Pour -oo et +oo :f(x) = [mx^3 + (m-2)x² + (m-1)x + m -3] / [ x^3 - 5x² + 6x ] -Si m est différent de 0 : Lim f(x) quand x tend vers -oo ou +oo = m -Si m = 0 : Lim f(x) quand x tend vers -oo ou +oo = 0 . * Pour 0 :- Si m > 3 : Lim f(x) quand x tend vers 0+ = +oo Lim f(x) quand x tend vers 0- = -oo - Si m = 3 : f(x) = [3x²+x+2]/[(x-2)(x-3)] Lim f(x) quand x tend vers 0 = 1/3 - Si m < 3 : Lim f(x) quand x tend vers 0+ = -oo Lim f(x) quand x tend vers 0- = +oo * Pour 2 : - Si m > 13/15 Lim f(x) quand x tend vers 2+ = -oo Lim f(x) quand x tend vers 2- = +oo - Si m = 13/15 f(x) = [13/15x^3 + (13/15 - 2) x² + (13/15 - 1 ) x + 13/15 - 3 ] / (x-3)(x-2)x = [(x-2) ( 17x/30 - 13x²/30 + 2/30)] / [(x-2)(x-3)x ] - 32/[15 x(x-3)(x-2)] = [17x/30 - 13x²/30 + 2/30]/(x-3)x -32/[15x(x-3)(x-2)] Lim f(x) quand x tend vers 2+ = +oo Lim f(x) quand x tend vers 2- = -oo - Si m<13/15 Lim f(x) quand x tend vers 2+ = +oo Lim f(x) quand x tend vers 2- = -oo * Pour 3 : Si m > 3/5 : Lim f(x) quand x tend vers 3+ = +oo Lim f(x) quand x tend vers 3- =-oo Si m = 3/5 : Meme procédure que pour Lim de f(x) quand x tend vers 2 et m = 13/15 , on obtient donc: [7x - 3x² - 2]/30(x-2)x - 12/[ 5(x-3)(x-2)x] Lim f(x) quand x tend vers 3+ = -oo Lim f(x) quand x tend vers 3- = +oo Si m < 3/5 : Lim f(x) quand x tend vers 3+ = -oo Lim f(x) quand x tend vers 3+ = +oo Voila , sauf erreur , j'espère que c'est bon 
Dernière édition par Mim le Mar 02 Aoû 2011, 14:35, édité 2 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Mar 26 Juil 2011, 19:33 Mar 26 Juil 2011, 19:33 | |
| Il y a quelques erreurs je vais te proposer leurs correction.
Dernière édition par expert_run le Mar 02 Aoû 2011, 14:18, édité 1 fois | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Mer 27 Juil 2011, 13:02 Mer 27 Juil 2011, 13:02 | |
| j'ai fais 2 erreurs sur l'exo précédent j'essaierais de les corriger et de postuler ma solution pour l'exo 2 plus tard dans l'aprem . | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Jeu 28 Juil 2011, 12:30 Jeu 28 Juil 2011, 12:30 | |
| En attendant la résolution du problème2: Je poste ces deux exercices. Exercice4:Soit f une fonction numérique définie par:  avec a un réel. 1- Déterminer l'ensemble de définition Df. 2-Calculer la limite de f(x) quand x tend vers +oo. 3-On suppose dans cette question que a=1 Calculer la limite de f(x) quand x tend vers 2+ et 2-. 4-On suppose dans cette question que a=3 Prouver que f admet une limite finie en 2 ; et déterminer cette limite. Exercice5:Calculer les limites suivantes:1-  2-  3-  | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Jeu 28 Juil 2011, 15:37 Jeu 28 Juil 2011, 15:37 | |
| Exercice 4 :
1)- Df={x £ IR / x^3 - 1 >= 0 ; x+2 >= 0 ; V(x+2) - 2 =/= 0 }
==> x^3 >= -1 ; x>= -2 ; x =/= 2
<=> Df = [-1;2[U]2;+oo[
2)- Lim f(x) quand x tend vers +oo :
Lim [Vx ( V(x²+1/Vx) - a/Vx ) ] / Vx (V(1+2/x) - 2/Vx ]
Lim ( V(x² + 1/Vx ) - a/Vx ) / ( V(1+2/x) - 2/Vx
comme Lim de a/Vx = Lim de 2/x = Lim de -2/Vx = 0 ( quand x tend vers +oo )
alors Lim f(x) quand x tend vers +oo = +oo
3)-Lim f(x) quand vers 2+ et 2- quand a = 1 :
Lim [ V(x^3 + 1) - 1 ] / V(x+2) - 2
quand x tend vers 2 + ; lim = +oo
quand x tend vers 2- ; lim = -oo
4)-Prouvons que f admet une limite finie en 2 quand a = 3 ; et déterminons cette limite:
On a 2 n'appartient pas a Df, donc pour prouver que f(x) admet une limite finie en 2 il nous faut montrer que Lim f(x) quand x tend vers 2+ = Lim f(x) quand x tend vers 2-
Lim [ V(x^3 + 1 ) - 3 ] / [ V(x+2) - 2 ]
= Lim [ ( V(x^3 + 1) - 3 ) (V (x^3 +1) + 3 ) ] / [ (V(x+2) - 2 ) ( V(x^3 +1) + 3 )
= Lim [ ( x^3 - 8 ) ( V(x+2) + 2 ) ] / [ ( x-2 ) ( V(x^3 +1) + 3 ) ]
= Lim [ ( x²+2x+4) ( V(x+2) + 2 ) ] / [ V(x^3 +1) + 3) ]
Observons que V(x^3 +1) + 3 ) est différent de 0 quand x tend vers 2
Ce qui fait que Lim2+ = Lim2- et que la fonction admet une limite finie
=8
Sauf erreur .
Dernière édition par Mim le Ven 29 Juil 2011, 14:50, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Jeu 28 Juil 2011, 20:24 Jeu 28 Juil 2011, 20:24 | |
| - Mim a écrit:
- Exercice 3 :
1)- Df = { x £ IR / x(x-2)(x-3) =/= 0 }
c'est à dire : x=/= 0 ; x =/= 2 ; x=/= 3
Df = ]-oo;0[U]0;2[U]2;3[U]3;+oo[
2)- Etudions les limites de f(x) aux bornes de Df :
*Pour -oo et +oo :
f(x) = [mx^3 + (m-2)x² + (m-1)x + m -3] / [ x^3 - 5x² + 6x ]
-Si m est différent de 0 :
Lim f(x) quand x tend vers -oo ou +oo = m
-Si m = 0 :
Lim f(x) quand x tend vers -oo ou +oo = 0 .
* Pour 0 :
- Si m > 3 :
Lim f(x) quand x tend vers 0+ = +oo
Lim f(x) quand x tend vers 0- = -oo
- Si m = 3 :
f(x) = [3x²+x+2]/[(x-2)(x-3)]
Lim f(x) quand x tend vers 0 = 1/3
- Si m < 3 :
Lim f(x) quand x tend vers 0+ = -oo
Lim f(x) quand x tend vers 0- = +oo
* Pour 2 :
- Si m > 13/15
Lim f(x) quand x tend vers 2+ = -oo
Lim f(x) quand x tend vers 2- = +oo
- Si m = 13/15
f(x) = [13/15x^3 + (13/15 - 2) x² + (13/15 - 1 ) x + 13/15 - 3 ] / (x-3)(x-2)x
= [(x-2) ( 17x/30 - 13x²/30 + 2/30)] / [(x-2)(x-3)x ] - 32/[15 x(x-3)(x-2)]
= [17x/30 - 13x²/30 + 2/30]/(x-3)x -32/[15x(x-3)(x-2)]
Lim f(x) quand x tend vers 2+ = +oo
Lim f(x) quand x tend vers 2- = -oo
- Si m<13/15
Lim f(x) quand x tend vers 2+ = +oo
Lim f(x) quand x tend vers 2- = -oo
* Pour 3 :
Si m > 3/5 :
Lim f(x) quand x tend vers 3+ = +oo
Lim f(x) quand x tend vers 3- =-oo
Si m = 3/5 :
Meme procédure que pour Lim de f(x) quand x tend vers 2 et m = 13/15 , on obtient donc:
[7x - 3x² - 2]/30(x-2)x - 12/[ 5(x-3)(x-2)x]
Lim f(x) quand x tend vers 3+ = -oo
Lim f(x) quand x tend vers 3- = +oo
Si m < 3/5 :
Lim f(x) quand x tend vers 3+ = -oo
Lim f(x) quand x tend vers 3+ = +oo
Voila , sauf erreur , j'espère que c'est bon  Ce qui est en rouge je pense qu'il est faux. | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Jeu 28 Juil 2011, 21:45 Jeu 28 Juil 2011, 21:45 | |
| Oui j'avais dis que j'avais 2 erreurs dans ma correction et que j'essayais de régler ça, j'éditerais ma solution quand j'en aurai une complète  | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Jeu 28 Juil 2011, 22:43 Jeu 28 Juil 2011, 22:43 | |
| Exercice 5 :
Limite n°3 :
on a quand x tend vers 4 : |x²-2x| = x²-2x
Lim ( x²-2x-8 )/(x²-5x+4)
x²-2x- 8 = ( x+2) (x-4)
x²-5x+4 = (x-1) (x-4)
Lim (x+2) / (x-1) = 2
Limite n° 1 :
Lim quand x tend vers + oo de : ( xV(4x²+3x-7) -2x²)
= Lim x [ (V4x²+3x-7) - 2x)]
= Lim x [ (4x²+3x-7 - 4x²) / ( V(4x²+3x-7) + 2x )
= Lim x [ x( 3 - 7/x) / x ( V(4+3/x-7/x²) + 2 ) ]
= Lim x [ ( 3-7/x) / ( V(4+3/x-7/x²) +2 ) ]
On sait que Lim 7/x = Lim 7/x² = Lim 3/x = 0, quand x tend vers +oo
en simplifiant on trouve que la Lim = +oo .
Limite n°2 :
Ca va etre un peu compliqué à lire mais je ne sais pas comment faire pour le latex alors j'essaierai de bien espacer pour clarifier:
f(x) = [ V(10x²+9) - 7] / [ V(x+2) -5 + V(x²+5) ]
= [ V(10x²+9) - 7] / [ V(x+2) -2 + V(x²+5) -3 ]
= [ V(10x²+9) - 7] / [ (x-2)/( V(x+2) + 2 ) +(x-2)(x+2) / ( V(x²+5) + 3 ) ]
= [ 10(x-2)(x+2) ] / [ ( V(10x²+9)+ 7) [ (x-2)/ ( V(x+2) +2) + (x-2)(x+2)/(V(x²+5)+3) ] ]
= [ 10(x+2) / [ ( V(10x²+9) + 7 ) / ( V(x+2) + 2 ) + [(V(10x²+9) + 7) (x+2)]/(V(x²+5) + 3) ]
Lim de f(x) quand x tend vers 2 = 240 / 77
Dernière édition par Mim le Ven 29 Juil 2011, 15:28, édité 1 fois | |
|
  | |
princessdesmaths
Maître

 Nombre de messages : 149 Nombre de messages : 149
Age : 29
Localisation : Casablanca
Date d'inscription : 24/09/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Jeu 28 Juil 2011, 22:58 Jeu 28 Juil 2011, 22:58 | |
| - expert_run a écrit:
- Comme prévu dans ce sujet nous allons attaquer la résolution des exercices de la leçon"Limites et continuité".
Si tous les forumistes intéressés par le préparation TSM ont le livre "AL MOUFIDE" on va bien progresser dans notre préparation.
Mais si c'est pas le cas on sera obligé de poster les énoncés des exercices sur le forum.
La durée de cette leçon sera précisée en compte de la participation des forumistes; car si la participation est médiocre on sera obligé d’étendre la durée de la leçon. Mais dès le début du Ramadan inchallah les durées seront limitées .
Les règles:
-Si on résout un exercice on ne passe à la résolution du suivant que si la solution du précédent s'avère juste.
-Si quelqu'un veut poster les solutions de plusieurs exercices en même temps il est préférable de les poster en spoiler.
-Les solutions des exercices doivent être complètes.
-SI quelqu'un poste un exercice différent de ceux dans le livre il est obligé d'indiquer qu'il est hors du livre.
Alors je vais poster le premier exercice (Mais si vous avez tous le livre Almoufide veuillez nous prévenir pour ne pas perdre le temps de recopier les énoncés des exercices). c'est preferable voir indisponsable de fixer une heure pour commencer selon chaque jour ! amicalement | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Jeu 28 Juil 2011, 23:02 Jeu 28 Juil 2011, 23:02 | |
| C'est comme un marathon fixer l'heure ne sert à rien. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 08:09 Ven 29 Juil 2011, 08:09 | |
| Ce qui est en rouge sont tes fautes que j'ai rectifier. - Mim a écrit:
- Exercice 3 :
1)- Df = { x £ IR / x(x-2)(x-3) =/= 0 }
c'est à dire : x=/= 0 ; x =/= 2 ; x=/= 3
Df = ]-oo;0[U]0;2[U]2;3[U]3;+oo[
2)- Etudions les limites de f(x) aux bornes de Df :
*Pour -oo et +oo :
f(x) = [mx^3 + (m-2)x² + (m-1)x + m -3] / [ x^3 - 5x² + 6x ]
-Si m est différent de 0 :
Lim f(x) quand x tend vers -oo ou +oo = m
-Si m = 0 :
Lim f(x) quand x tend vers -oo ou +oo = 0 .
* Pour 0 :
- Si m > 3 :
Lim f(x) quand x tend vers 0+ = +oo
Lim f(x) quand x tend vers 0- = -oo
- Si m = 3 :
f(x) = [3x²+x+2]/[(x-2)(x-3)]
Lim f(x) quand x tend vers 0 = 1/3
- Si m < 3 :
Lim f(x) quand x tend vers 0+ = -oo
Lim f(x) quand x tend vers 0- = +oo
* Pour 2 :
- Si m > 13/15
Lim f(x) quand x tend vers 2+ = -oo
Lim f(x) quand x tend vers 2- = +oo
- Si m = 13/15
f(x) = [13/15x^3 + (13/15 - 2) x² + (13/15 - 1 ) x + 13/15 - 3 ] / (x-3)(x-2)x
=(13x^(3)-17x^(2)-2x-32)/x(x-2)(x-3)
= (13x^(2)+9x+16)/x(x-3)
Lim f(x) quand x tend vers 2= -43
- Si m<13/15
Lim f(x) quand x tend vers 2+ = +oo
Lim f(x) quand x tend vers 2- = -oo
* Pour 3 :
Si m > 3/5 :
Lim f(x) quand x tend vers 3+ = +oo
Lim f(x) quand x tend vers 3- =-oo
Si m = 3/5 :
Meme procédure que pour Lim de f(x) quand x tend vers 2 et m = 13/15 , on obtient donc:
(3x^(3)-7x^(2)-2x-12)/(5x(x-2)(x-3)=(3x^(2)+2x+4)/5x(x-2)
Lim f(x) quand x tend vers 3= 37/15
Si m < 3/5 :
Lim f(x) quand x tend vers 3+ = -oo
Lim f(x) quand x tend vers 3- = +oo
Voila , sauf erreur , j'espère que c'est bon  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 08:31 Ven 29 Juil 2011, 08:31 | |
| - Mim a écrit:
- Exercice 4 :
1)- Df={x £ IR / x^3 - 1 >= 0 ; x+2 >= 0 ; V(x+2) - 2 =/= 0 }
==> x^3 >= -1 ; x>= -2 ; x =/= 2
<=> Df = [-1;2[U]2;+oo[
2)- Lim f(x) quand x tend vers +oo :
Lim [Vx ( V(x²+1/Vx) - a/Vx ) ] / Vx (V(1+2/x) - 2/Vx ]
Lim ( V(x² + 1/Vx ) - a/Vx ) / ( V(1+2/x) - 2/Vx
comme Lim de a/Vx = Lim de 2/x = Lim de -2/Vx = 0 ( quand x tend vers +oo )
alors Lim f(x) quand x tend vers +oo = +oo
3)-Lim f(x) quand vers 2+ et 2- quand a = 1 :
Lim [ V(x^3 + 1) - 1 ] / V(x+2) - 2
quand x tend vers 2 + ; lim = +oo
quand x tend vers 2- ; lim = -oo
4)-Prouvons que f admet une limite finie en 2 quand a = 3 ; et déterminons cette limite:
On a 2 n'appartient pas a Df, donc pour prouver que f(x) admet une limite finie en 2 il nous faut montrer que Lim f(x) quand x tend vers 2+ = Lim f(x) quand x tend vers 2-
Lim [ V(x^3 + 1 ) - 3 ] / [ V(x+2) - 2 ]
= Lim [ ( V(x^3 + 1) - 3 ) (V (x^3 +1) + 3 ) ] / [ (V(x+2) - 2 ) ( V(x^3 +1) + 3 )
= Lim [ ( x^3 - 8 ) ( V(x+2) + 2 ) ] / [ ( x-2 ) ( V(x^3 +1) + 3 ) ]
= Lim [ ( x²+2x+4) ( V(x+2) + 2 ) ] / [ V(x^3 +1) + 3) ]
Observons que V(x^3 +1) + 3 ) est différent de 0 quand x tend vers 2
Ce qui fait que Lim2+ = Lim2- et que la fonction admet une limite finie
=5/3
Sauf erreur . Je te félicite tout d'abord pour ta participation dans cette préparation ; qui malheureusement connait une participation médiocre. Pour ta solution je crois qu'il y a une petite erreur à la fin . lim f(x) quand x tend vers 2 est 8 et pas 5/3 | |
|
  | |
princessdesmaths
Maître

 Nombre de messages : 149 Nombre de messages : 149
Age : 29
Localisation : Casablanca
Date d'inscription : 24/09/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 12:20 Ven 29 Juil 2011, 12:20 | |
| - expert_run a écrit:
- C'est comme un marathon fixer l'heure ne sert à rien.
dans tous les marathon on fait le depart en meme temps , l'heure du depart est toujours fixée , c'est ce que je voulais dire , en tout cas l'organisation facilite le travail . amicalement | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 13:12 Ven 29 Juil 2011, 13:12 | |
| Vu qu'on avait deja commencé sur un autre poste, il n'a fait que postuler des exercices ici, maintenant il y a encore des exo sans solutions ( exercice 2 ; 2 sous cas dans l'exercice 3, une limite dans l'exercice 5 ) donc pas besoin de fixer un horraire juste pour postuler une solution pour un exercice  , j'espère que tu vas participer a la résolution des exercices avec nous, amicalement . | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 13:30 Ven 29 Juil 2011, 13:30 | |
| - expert_run a écrit:
- Ce qui est en rouge sont tes fautes que j'ai rectifier.
- Mim a écrit:
- Exercice 3 :
- Si m = 13/15
f(x) = [13/15x^3 + (13/15 - 2) x² + (13/15 - 1 ) x + 13/15 - 3 ] / (x-3)(x-2)x
=(13x^(3)-17x^(2)-2x-32)/x(x-2)(x-3)
= (13x^(2)+9x+16)/x(x-3)
Lim f(x) quand x tend vers 2= -43
Tu as a ton tour commis une petite erreur aussi là dessus car tu as oublié de mettre le 15 en bas de la fraction ca donnera : f(x) = (13x² +9x + 16)/[ 15(x-3)x] Lim quand x tend vers 2= -52/15 En ce qui concerne l'exercice 4 c'est bel et bien 8 j'avais fais une petite faute d'empressement en arrivant vers la fin ! | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 13:36 Ven 29 Juil 2011, 13:36 | |
| Ah t a raison mais Lim quand x tend vers 2= -43/15 et pas 52/15 | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 14:48 Ven 29 Juil 2011, 14:48 | |
| on trouve -104/30 ce qui fait -52/15 il me semble que c'est bien cela ! | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 15:29 Ven 29 Juil 2011, 15:29 | |
| Message édité dans la 2ème page , solution de la 2ème limite de l'exercice 5 ajoutée , au plaisir ! | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Ven 29 Juil 2011, 20:10 Ven 29 Juil 2011, 20:10 | |
| Pour l'exercice 5 ta solution est exacte. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Sam 30 Juil 2011, 14:01 Sam 30 Juil 2011, 14:01 | |
| L'exercice 2 reste à faire on doit pas l'oublier alors je poste les exercices suivants. Exercice 6 et 7:
- Spoiler:
Déterminer les limites suivantes:1)-  2)-  3)-  4)-  5)-  6)-  7)-  8-  9)- 
| |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Sam 30 Juil 2011, 15:42 Sam 30 Juil 2011, 15:42 | |
| Solution exercice 6 et 7:- Spoiler:
1-  2-  3-  Cette dernière limite ne s'affiche pas correctement chez moi ; alors si vous avez le même problème vous pouvez voir la solution ici: [url]http://latex.codecogs.com/gif.latex?\lim_{-\infty&space;}\frac{\sqrt{x^{4}+1}-\sqrt{x^{4}-1}}{\sqrt{x^{2}+1}-\sqrt{x^{2}-1}}=\lim_{-\infty&space;}-x\frac{\sqrt{1+\frac{1}{x^{4}}}-\sqrt{1-\frac{1}{x^{4}}}}{\sqrt{1+\frac{1}{x^{2}}}-\sqrt{1-\frac{1}{x^{2}}}}=\lim_{-\infty&space;}\frac{\frac{-2}{x^{3}}}{(\sqrt{1+\frac{1}{x^{2}}}-\sqrt{1-\frac{1}{x^{2}}}).(\sqrt{1+\frac{1}{x^{4}}}+\sqrt{1-\frac{1}{x^{4}}})}=\lim_{-\infty&space;}\frac{(\sqrt{1+\frac{1}{x^{2}}}+\sqrt{1-\frac{1}{x^{2}}}).(\frac{-2}{x^{3}})}{(\frac{2}{x^{2}})(\sqrt{1+\frac{1}{x^{4}}}+\sqrt{1-\frac{1}{x^{4}}})}=0[/url]
| |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  Sam 30 Juil 2011, 21:17 Sam 30 Juil 2011, 21:17 | |
| Voici la troisième qui ne s'affiche pas: .(\sqrt{1+\frac{1}{x^{4}}}+\sqrt{1-\frac{1}{x^{4}}})}=\lim_{-\infty&space;}\frac{(\sqrt{1+\frac{1}{x^{2}}}+\sqrt{1-\frac{1}{x^{2}}}).(\frac{-2}{x^{3}})}{(\frac{2}{x^{2}})(\sqrt{1+\frac{1}{x^{4}}}+\sqrt{1-\frac{1}{x^{4}}})}=0) Je vois que c'est juste! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices. Sujet: Re: Préparation TSM:: L-1/Limites et continuité:p/Exercices.  | |
| |
|
  | |
| | Préparation TSM:: L-1/Limites et continuité:p/Exercices. |  |
|
