Préparation TSM:: L-1/Limites et continuité:p/Exercices.

Solution pou 6:
On pose I={f(X_1);....;f(X_n)}
Donc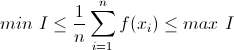

et puisque f est continue sur [a;b] donc il existe c de [a;b] tq:

ali-mes a écrit:

Exercice 1:

Etudier la continuité de la fonction f définie sur l'intervalle ]0,1] tel que:
Exercice 5:

Soit f une fonction continue et positive sur IR+ tel que: .

Montrer que l'équation f(x)=x admet au moins une solution dans IR+.

Je pense que f est une fonction continue et strictement positive sur IR+

expert_run a écrit:

ali-mes a écrit:

Exercice 1:

Etudier la continuité de la fonction f définie sur l'intervalle ]0,1] tel que:
Exercice 5:

Soit f une fonction continue et positive sur IR+ tel que: .

Montrer que l'équation f(x)=x admet au moins une solution dans IR+.

Je pense que f est une fonction continue et strictement positive sur IR+

D'après l'énoncé, c'est: IR+ متصلة و موجبة على(comme j'ai déjà écrit), et pas: IR+ متصلة و موجبة قطعاعلى

Ok je vais essayer.

En attendant la résolution des exercices postulés par ali-mes ; on termine avec les exercices du livre.
Exercice 87:
Soit E l'ensemble des fonctions numériques f définies sur IR et vérifiant la propriété (P) suivante:
(P): (pr tt (x;y)€IR^2) |f(x)-f(y)|=|x-y|
1-a- Démontrer que pr tt f de E; la fonction f est continue sur IR.
b- Prouver que pr tt f de E; la fonction f est injective.
c- Soit f de E, prouvez que la fonction f est strictement monotone sur IR.
2- Déterminer l'ensemble E.
Exercice 88:
f est une fonction numérique définie de [a;b] vers [a;b] tq:
pr tt (x;t)€[a;b] ^2 : |f(x)-f(t)|<|x-t|
1- Prouver que f est continue sur [a;b].
2- Prouver que f admet un point fixe dans [a;b].

1)-a- mettons y = 0 , on obtient que : |f(x)-f(0)|=|x|
on aura donc f(x)-f(0) = -x ou f(x)-f(0)=x , donc les 2 cas on aura f(x) une fonction affine tel que f(x) = ax + k et donc f est continue sur IR .

b-Prouvons que f est injective et donc que f(x)=f(y) => x=y :
on a f(x)=f(y) => f(x)-f(y) = 0
=> |f(x)-f(y)| = 0
=> |x-y| = 0
=> x = y
CQFD .

c-on a f(x) est continue sur IR et injective sur IR, donc f(x) est strictement monotone sur IR .
2ème méthode comme on a f(x) une fonction affine alors : on a T = ( f(x)-f(y) ) / (x-y) , donc puisque |f(x)-f(y)|=|x-y| alors T=1 ou -1 et donc f est strictement monotone quelque soit (x,y) de IR² .

2)-l'ensemble E , {x £ IR / f : x --> -x+K , f : x---> x+K ( tel que K une constante réelle dans IR) }

Solution pour 88:
1--Soit x_0 €[a;b]
Et puisque lim(x-->x_0)|x-x_0|=0
Donc lim(x-->x_0)f(x)-f(x_0)=0==>lim(x-->x_0)f(x)=f(x_0)
Alors f est continue sur [a;b].
2-- C'est une simple déduction de l'exercice 70.

Exercice 89:
Soient f et g de fonction de [0;1] vers [0;1] tq f et g sont continues sur [0;1] .
on suppose que pr tt x€[0;1] fog(x)=gof(x)
Prouver qu'il existe a €[0;1] tq; f(a)=g(a)

l'exercice 89 est trop compliqué je crois que j 'aurai besoin d'un petit aide.

solution pour l’exercice 89 :
On raisonne par l'absurde.
On suppose que pr tt x€[0;1] f(x)=/=g(x)
On note H(x)=f(x)-g(x) et puisque H(x)=0 n'admet pas de solution et f et g sont continues
Alors on peut supposer par symétrie que pr tt x€[0;1] f(x)>g(x)
Donc il existe d appartenant à IR*+ tq pp tt x€[0;1] f(x)>=g(x)+d

Revenons à l'hypothèse:
pr tt x€[0;1] fog(x)=gof(x)
Donc fogof=gofof ==>fofog=gofof
fofogof=gofofof ==> fofofog=gofofof
|
|
|
Alors

(Une petite récurrence reste utile mais je la laisse au lecteur)

Ainsi
f(x)>=g(x)+d
fof(x)>=gof(x)+d=fog(x)+d>=gog(x)+2d
fofof(x)>=gog(f(x))+2d>=gogog(x)+3d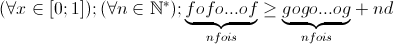
|
|
|

(Ici aussi une récurrence reste utile)
Donc

Ce qui est absurde.
Donc il existe a €[0;1] tq; f(a)=g(a)

L'exercice 90 est déjà postulé par ali-mes. Donc on passe directement à l'exercice 91.
Exercice 91:
Soit f une fonction continue sur [0;1] et f(0)=f(1)
pr tt n€IN et n>=2; on considère la fonction numérique fn définie sur [0;1-(1/n)] par :
fn(x)=f(x+(1/n))-f(x)
1-- Calculer
2- Prouver qu'il existe c de ]0;1[ tq: f(c)=f(c+(1/n))

Solution pour 91:

1-

2- la fonction fn est continue sur [0;1-(1/n)] donc fn est bornée sur J= [0;1-(1/n)]
On pose M=Max(x€J) fn(x) et m=min(x€J) fn(x)
Donc

ET d'apres TVI il existe c tel que :

D'où la conclusion.

Exercice 92:
f est une fonction continue et positive sur IR+ tq : lim(x-->+oo)(f(x)/x)=1
Prouver que l'équation f(x)=x admet au moins une solution dans IR+
Exercice 93:
f est une fonction numérique définie sur [0;1] et f(1)<0<f(0)
On suppose qu'il existe une fonction numérique g continue sur [0;1] tq f+g est croissante.
Prouver qu'il existe c €[0;1] tq: f(c)=0

Je crois qu'il y a une erreur dans l'exercice 92:

On pose f(x)=x+1 donc f est continue et positive sur IR+ tq : lim(x-->+oo)(f(x)/x)=1

Alors f(x)=0 ==>x=-1 (Et on a x€IR+)

Donc je pense que l'exercice est faux .

[quote="expert_run"]Exercice 92:
f est une fonction continue et positive sur IR+ tq : lim(x-->+oo)(f(x)/x)=1
Prouver que l'équation f(x)=x admet au moins une solution dans IR+


c'est f(x)=x ou f(x)=0 ??

Ah oui f(x)=x
Mais même si f(x)=x
on aura
On pose f(x)=x+1 donc f est continue et positive sur IR+ tq : lim(x-->+oo)(f(x)/x)=1

Alors f(x)=x ==>x=x+1 ==> 1=0 ' CE QUI EST FAUX"

Donc je pense que l'exercice est faux .

oui,mais il y a écris "au moins une solution"
donc si je ne me trompe
en posant:
f(x)=(x²-2x+1)/x+2
on aura ,f(x)=x ==> x=1/4>0
??

En attendant la solution de l'exercice 93. Je poste les 4 deniers exercices (Pour 94 Je le posterai après).
Exercice 95:

Soit f une fonction définie et croissante sur [0;1]. On suppose que qlqs les nombres x;y;z et t tq: 0=<x<y<z<t on a :


Prouver que f est continue sur [0;1[

Exercice 96:
f et g deux fonctions continues sur le même intervalle I tel que :

pr tt x€I : (f(x))^2= (g(x))^2 =/= 0
Prouver que:
pr tt x€I: f(x)=g(x) ou pr tt x€I: f(x)=-g(x)

Exercice 97:
f est une fonction continue sur IR et vérifiant:
pr tt x€I : f(|x|)=|f(x)|>0
Prouver que f est paire .

Exercice 98:
Prouver qu'il existe une fonction f continue sur [0;2pi[ ; non constante et différente de x-->x tel que :
pr tt (x;y)€ [0;2pi[^2 : cos(x-y)=<cos(f(x)-f(y))

manazerty a écrit:

oui,mais il y a écris "au moins une solution"
donc si je ne me trompe
en posant:
f(x)=(x²-2x+1)/x+2
on aura ,f(x)=x ==> x=1/4>0
??

La question est de montrer que pour toute fonction vérifiant les conditions de l'exercice
l'équation f(x)=x admet au moins une solution.
Le truc que t'avait dis rend l'exercice banale alors que lui il figure parmi les exercices qui demande un peu de réflexion.

salut Mateux ,voila l ennonce correct de l exo 92 p 44
[img][/img]

pardon ,f est positive

Merci.Alors je vois qu'il figure parmi les exercices postulés par Ali-mes.

solution d'exercice 92

[img][/img]
AmiCalemenT

Je pense que l'exercice 96 est faux. Si les deux fonctions se coupe en un point appartenant à (OX). Donc il faut ajouter que f(x)#0

j'aime maths a écrit:

solution d'exercice 92

[img][/img]
AmiCalemenT

Oui c'est juste.J'ai fait les même étapes .