Préparation TSM:: L-1/Limites et continuité:p/Exercices.

Comme prévu dans ce sujet nous allons attaquer la résolution des exercices de la leçon"Limites et continuité".
Si tous les forumistes intéressés par le préparation TSM ont le livre "AL MOUFIDE" on va bien progresser dans notre préparation.
Mais si c'est pas le cas on sera obligé de poster les énoncés des exercices sur le forum.
La durée de cette leçon sera précisée en compte de la participation des forumistes; car si la participation est médiocre on sera obligé d’étendre la durée de la leçon. Mais dès le début du Ramadan inchallah les durées seront limitées .

Les règles:
-Si on résout un exercice on ne passe à la résolution du suivant que si la solution du précédent s'avère juste.
-Si quelqu'un veut poster les solutions de plusieurs exercices en même temps il est préférable de les poster en spoiler.
-Les solutions des exercices doivent être complètes.
-SI quelqu'un poste un exercice différent de ceux dans le livre il est obligé d'indiquer qu'il est hors du livre.

Alors je vais poster le premier exercice (Mais si vous avez tous le livre Almoufide veuillez nous prévenir pour ne pas perdre le temps de recopier les énoncés des exercices).

Exercice1:

Pour tout entier relatif n, on considère la fonction numérique définie par:

Déterminez selon les valeurs de n l'ensemble de définition de la fonction et calculez les limites de aux bornes de .

Bonne chance :p >>

Déjà posté ici, non?: :p
https://mathsmaroc.jeun.fr/t18183p30-preparation-tsm

oui ca c de l'organisation maintenant on progressera bien

kaj mima a écrit:

Déjà posté ici, non?: :p
https://mathsmaroc.jeun.fr/t18183p30-preparation-tsm

Ta réponse est incomplète t'a pas étudié la limite de f(x) quand x tend vers 0 dans le cas où n<0.

Solution:

Dans le cas ou n > 0 :
On obtient : Df = ]-oo;+oo[

*Lim f(x) quand x tend vers +oo:
On aura toujours la puissance de 3x > a celle de 5x ce qui fait que Lim f(x) quand x tend vers +oo est de +oo .


*Lim f(x) quand x tend vers -oo :

La encore on aura toujours la puissance de 3x > a celle de 5x
Cependant il faudra voir si cette puissance est paire ou impaire :

-dans le cas ou n = 2k ( avec k appartenant a IN )
Lim f(x) quand x tend vers -oo est -oo .

-dans le cas ou n = 2k+1 ( avc k appartenant a IN)
Lim f(x) quand x tend vers -oo est +oo

Dans le cas ou n=0 :
Là aussi on obtient Df = ]-oo,+oo[

Lim f(x) quand x tend vers +oo = +oo
Lim f(x) quand x tend vers -oo = -oo


Dans le cas ou n=< 0
On a Df = ]-oo, +oo[

*Lim f(x) quand x tend vers +oo ;trois possibilités se présentent :

-Si -3<n<0 :
La Lim de f(x) quand x tend vers +oo est de +oo
-Si n=-3
La lim de f(x) quand x tend vers +oo est de -11
-Si n=< -4
La lim de f(x) quand x tend vers +oo est de -14 .

*Lim f(x) quand x tend vers -oo :
- Si n = -1
La lim de f(x) quand x tend vers -oo est de + oo
- Si n= -2
La lim de f(x) quand x tend vers -oo est de -oo
- Si n = -3
La lim de f(x) quand x tend vers -oo est de-11
- Si n =< -4
La lim de f(x) quand x tend vers -oo est de -14


Ceci est ma solution pour cet exercice, en espérant avoir bien raisonné , j'attends vos réactions et les prochains exos !
[i]

Mim a écrit:

Solution:

Dans le cas ou n=< 0
On a Df = ]-oo, +oo[
*Lim f(x) quand x tend vers +oo ;trois possibilités se présentent :

-Si -3<n<0 :
La Lim de f(x) quand x tend vers +oo est de +oo
-Si n=-3
La lim de f(x) quand x tend vers +oo est de -11
-Si n=< -4
La lim de f(x) quand x tend vers +oo est de -14 .

*Lim f(x) quand x tend vers -oo :
- Si n = -1
La lim de f(x) quand x tend vers -oo est de + oo
- Si n= -2
La lim de f(x) quand x tend vers -oo est de -oo
- Si n = -3
La lim de f(x) quand x tend vers -oo est de-11
- Si n =< -4
La lim de f(x) quand x tend vers -oo est de -14


Ceci est ma solution pour cet exercice, en espérant avoir bien raisonné , j'attends vos réactions et les prochains exos !
[i]

D'abord, quand n<0 le domaine de définition est ]-oo,0[ U ]0,+oo[
Et puis donc il faut étudier aussi le cas quand x tend vers 0.
Donc je termine à mon tour:
n<0:

Si n est pair:
La lim de f(x) quand x tend vers 0+ est -oo.
La lim de f(x) quand x tend vers 0- est -oo.
Si n est impair:
La lim de f(x) quand x tend vers 0+ est -oo.
La lim de f(x) quand x tend vers 0- est +oo.

Sauf erreur!

.

Mim a écrit:

kaj mima a écrit:

D'abord, quand n<0 le domaine de définition est ]-oo,0[ U ]0,+oo[
Et puis donc il faut étudier aussi le cas quand x tend vers 0.

Oui t'as raison , celà dit je propose une approche différente a la tienne :

Soit f(x) = 3x ^ (n +3) - 5x ^(n) -14
= 3x^3 - 5 - 14/(x^n)* Quand x tend vers 0+ :
Lim x^n = +oo et donc Lim f(x) quand x tend vers 0+ est = -5

*Quand x tend vers 0- :
Lim f(x) quand x tend vers 0- = -5

J'attends votre avis

Comment tu as passé de la première ligne à la deuxième??

Oula j'ai fais une grosse gaffe o_o,
Je supprime mon post , je repostulerais ma réponse quand j'en aurais une , merci pour ta remarque kaj !

Pas grave!
Il faut qu'on passe à l'exercice 2 maintenant (enfin, il faut qu'il s'avère très bien que ce premier est bien complet!)

kaj mima a écrit:

Tu pourrais stp développer comment tu es arrivée a cette expression a partir de la fonction initiale, c'est flou pour moi , merci d'avance

C'est très simple:
3 x^(n+3)= 3 x^3 * x^(n) = 3 x^3 / x^(-n)
et 5^n= 5/x^(-n)
et par conséquent: f(x)= (3x^3 -5)/x^(-n) -14

Que quelqu'un postule un autre exercice pour avancer ( on a bsoin de plus d'activité !!!! )

Ok je vais envoyer 3 exercice en même temps.

On attends toujours !

Exercice2:
Soit a un réel et la fonction numérique définie par: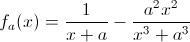

1-Déterminer l'ensemble de définition de .
2-Déterminer les valeurs de a pour que admet une limite en -a.
Exercice3:
Soient m un réel et f le fonction numérique définie par:

1-Déterminer l’ensemble de définition de la fonction f .
2-Étudier les limites de f aux bornes de l'ensemble de définition selon les valeurs de m.

Exercice 2:

expert_run a écrit:

Exercice2:
Soit a un réel et la fonction numérique définie par:

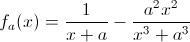
1-Déterminer l'ensemble de définition de .
2-Déterminer les valeurs de a pour que admet une limite en -a.

1)-Df={x £ IR/x+a =/= 0 et x^3 + a^3 =/= 0}
Df= IR-{-a}

2)-On doit trouver les valeurs de a pour que f(x) admette une limite finie en -a :
f(x) = 1/(x+a) - (x²a²)/(x^3+a^3)
= (x²-ax+a² -x²a²)/(x^3+a^3)
on a lim x^3 + a^3 quand x tend vers -a = 0
donc pour que f(x) admette une limite finie vers -a il nous faut simplifier par (x+a), et donc lim x²-ax+a²-a²x² doit etre =0 pour -a
x²-ax+a²-a²x² = 0 <=> a² +a²+a² - a^4 = 0
<=> 3a² = a^4
<=> a = V3 ou a = -V3 ou a = 0 .

pour le cas de a = 0
on aura lim 1/x = +/- oo donc ce n'est pas une solution valable.

pour le cas de a=V3 : ( et donc -a = -V3 hein ! )
f(x) = ( x² -V3x + 3-3x²)/(x+V3)(x²+3-V3 x)
Lima- ( -2x²-V3x + 3)/(x+V3)(x²+3-V3 x)
Lima- ( x+V3)(-2x+V3)/(x+V3)(x²+3-V3x)
Lima- (-2x+V3)/(x²+3-V3x)
=V3/3

pour le cas de a=-V3 ( et donc -a=V3)
f(x) = (x²+3+V3x-3x²)/(x-V3)(x²+3+V3x)
Lima- ( x-V3)(-2x-V3)/(x-V3)(x²+3+V3x)
=-V3

donc les valeurs de a sont : V3 et -V3

Exercice 3 :

1)- Df = { x £ IR / x(x-2)(x-3) =/= 0 }
c'est à dire : x=/= 0 ; x =/= 2 ; x=/= 3
Df = ]-oo;0[U]0;2[U]2;3[U]3;+oo[

2)- Etudions les limites de f(x) aux bornes de Df :

*Pour -oo et +oo :
f(x) = [mx^3 + (m-2)x² + (m-1)x + m -3] / [ x^3 - 5x² + 6x ]
-Si m est différent de 0 :
Lim f(x) quand x tend vers -oo ou +oo = m
-Si m = 0 :
Lim f(x) quand x tend vers -oo ou +oo = 0 .

* Pour 0 :
- Si m > 3 :
Lim f(x) quand x tend vers 0+ = +oo
Lim f(x) quand x tend vers 0- = -oo
- Si m = 3 :
f(x) = [3x²+x+2]/[(x-2)(x-3)]
Lim f(x) quand x tend vers 0 = 1/3
- Si m < 3 :
Lim f(x) quand x tend vers 0+ = -oo
Lim f(x) quand x tend vers 0- = +oo

* Pour 2 :
- Si m > 13/15
Lim f(x) quand x tend vers 2+ = -oo
Lim f(x) quand x tend vers 2- = +oo
- Si m = 13/15
f(x) = [13/15x^3 + (13/15 - 2) x² + (13/15 - 1 ) x + 13/15 - 3 ] / (x-3)(x-2)x
= [(x-2) ( 17x/30 - 13x²/30 + 2/30)] / [(x-2)(x-3)x ] - 32/[15 x(x-3)(x-2)]
= [17x/30 - 13x²/30 + 2/30]/(x-3)x -32/[15x(x-3)(x-2)]
Lim f(x) quand x tend vers 2+ = +oo
Lim f(x) quand x tend vers 2- = -oo
- Si m<13/15
Lim f(x) quand x tend vers 2+ = +oo
Lim f(x) quand x tend vers 2- = -oo

* Pour 3 :
Si m > 3/5 :
Lim f(x) quand x tend vers 3+ = +oo
Lim f(x) quand x tend vers 3- =-oo
Si m = 3/5 :
Meme procédure que pour Lim de f(x) quand x tend vers 2 et m = 13/15 , on obtient donc:
[7x - 3x² - 2]/30(x-2)x - 12/[ 5(x-3)(x-2)x]
Lim f(x) quand x tend vers 3+ = -oo
Lim f(x) quand x tend vers 3- = +oo
Si m < 3/5 :
Lim f(x) quand x tend vers 3+ = -oo
Lim f(x) quand x tend vers 3+ = +oo

Voila , sauf erreur , j'espère que c'est bon

Il y a quelques erreurs je vais te proposer leurs correction.

j'ai fais 2 erreurs sur l'exo précédent j'essaierais de les corriger et de postuler ma solution pour l'exo 2 plus tard dans l'aprem .

En attendant la résolution du problème2:
Je poste ces deux exercices.
Exercice4:
Soit f une fonction numérique définie par: avec a un réel.
1- Déterminer l'ensemble de définition Df.
2-Calculer la limite de f(x) quand x tend vers +oo.
3-On suppose dans cette question que a=1
Calculer la limite de f(x) quand x tend vers 2+ et 2-.
4-On suppose dans cette question que a=3
Prouver que f admet une limite finie en 2 ; et déterminer cette limite.

Exercice5:
Calculer les limites suivantes:
1-

2-

3-

Exercice 4 :

1)- Df={x £ IR / x^3 - 1 >= 0 ; x+2 >= 0 ; V(x+2) - 2 =/= 0 }
==> x^3 >= -1 ; x>= -2 ; x =/= 2
<=> Df = [-1;2[U]2;+oo[

2)- Lim f(x) quand x tend vers +oo :
Lim [Vx ( V(x²+1/Vx) - a/Vx ) ] / Vx (V(1+2/x) - 2/Vx ]
Lim ( V(x² + 1/Vx ) - a/Vx ) / ( V(1+2/x) - 2/Vx
comme Lim de a/Vx = Lim de 2/x = Lim de -2/Vx = 0 ( quand x tend vers +oo )
alors Lim f(x) quand x tend vers +oo = +oo

3)-Lim f(x) quand vers 2+ et 2- quand a = 1 :
Lim [ V(x^3 + 1) - 1 ] / V(x+2) - 2
quand x tend vers 2 + ; lim = +oo
quand x tend vers 2- ; lim = -oo

4)-Prouvons que f admet une limite finie en 2 quand a = 3 ; et déterminons cette limite:
On a 2 n'appartient pas a Df, donc pour prouver que f(x) admet une limite finie en 2 il nous faut montrer que Lim f(x) quand x tend vers 2+ = Lim f(x) quand x tend vers 2-

Lim [ V(x^3 + 1 ) - 3 ] / [ V(x+2) - 2 ]
= Lim [ ( V(x^3 + 1) - 3 ) (V (x^3 +1) + 3 ) ] / [ (V(x+2) - 2 ) ( V(x^3 +1) + 3 )
= Lim [ ( x^3 - 8 ) ( V(x+2) + 2 ) ] / [ ( x-2 ) ( V(x^3 +1) + 3 ) ]
= Lim [ ( x²+2x+4) ( V(x+2) + 2 ) ] / [ V(x^3 +1) + 3) ]

Observons que V(x^3 +1) + 3 ) est différent de 0 quand x tend vers 2
Ce qui fait que Lim2+ = Lim2- et que la fonction admet une limite finie

=8

Sauf erreur .

Mim a écrit:

Exercice 3 :

1)- Df = { x £ IR / x(x-2)(x-3) =/= 0 }
c'est à dire : x=/= 0 ; x =/= 2 ; x=/= 3
Df = ]-oo;0[U]0;2[U]2;3[U]3;+oo[

2)- Etudions les limites de f(x) aux bornes de Df :

*Pour -oo et +oo :
f(x) = [mx^3 + (m-2)x² + (m-1)x + m -3] / [ x^3 - 5x² + 6x ]
-Si m est différent de 0 :
Lim f(x) quand x tend vers -oo ou +oo = m
-Si m = 0 :
Lim f(x) quand x tend vers -oo ou +oo = 0 .

* Pour 0 :
- Si m > 3 :
Lim f(x) quand x tend vers 0+ = +oo
Lim f(x) quand x tend vers 0- = -oo
- Si m = 3 :
f(x) = [3x²+x+2]/[(x-2)(x-3)]
Lim f(x) quand x tend vers 0 = 1/3
- Si m < 3 :
Lim f(x) quand x tend vers 0+ = -oo
Lim f(x) quand x tend vers 0- = +oo

* Pour 2 :
- Si m > 13/15
Lim f(x) quand x tend vers 2+ = -oo
Lim f(x) quand x tend vers 2- = +oo
- Si m = 13/15
f(x) = [13/15x^3 + (13/15 - 2) x² + (13/15 - 1 ) x + 13/15 - 3 ] / (x-3)(x-2)x
= [(x-2) ( 17x/30 - 13x²/30 + 2/30)] / [(x-2)(x-3)x ] - 32/[15 x(x-3)(x-2)]
= [17x/30 - 13x²/30 + 2/30]/(x-3)x -32/[15x(x-3)(x-2)]
Lim f(x) quand x tend vers 2+ = +oo
Lim f(x) quand x tend vers 2- = -oo
- Si m<13/15
Lim f(x) quand x tend vers 2+ = +oo
Lim f(x) quand x tend vers 2- = -oo

* Pour 3 :
Si m > 3/5 :
Lim f(x) quand x tend vers 3+ = +oo
Lim f(x) quand x tend vers 3- =-oo
Si m = 3/5 :
Meme procédure que pour Lim de f(x) quand x tend vers 2 et m = 13/15 , on obtient donc:
[7x - 3x² - 2]/30(x-2)x - 12/[ 5(x-3)(x-2)x]
Lim f(x) quand x tend vers 3+ = -oo
Lim f(x) quand x tend vers 3- = +oo
Si m < 3/5 :
Lim f(x) quand x tend vers 3+ = -oo
Lim f(x) quand x tend vers 3+ = +oo

Voila , sauf erreur , j'espère que c'est bon

Ce qui est en rouge je pense qu'il est faux.

Oui j'avais dis que j'avais 2 erreurs dans ma correction et que j'essayais de régler ça, j'éditerais ma solution quand j'en aurai une complète