| | Préparations aux olympiades de Terminale (2012) |  |
|
+23rimele judicecharatein mohamed diai yasserito tahasinbad the kiler darkpseudo Incompri M.Marjani boubou math samsoum05 kaj mima manazerty Misterayyoub nmo mr.mertasayeker az360 expert_run xyzakaria Othmaann ali-mes n.naoufal Mehdi.O 27 participants |
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 17 Sep 2011, 19:04 Sam 17 Sep 2011, 19:04 | |
| nmo a toujours des jolis problèmes à nous proposer  , j'ai pas encore fait le côté gauche de l'inégalité, mais voici ma réponse au côté droit: J'ai procédé presque avec la même méthode que j'ai fait ici: https://mathsmaroc.jeun.fr/t18326-jolie-ingealite-geometrique.Premièrement, on note D, E et F les points du contact du cercle inscrit au triangle ABC avec les cotès [BC], [AC] et [AB] respectivement.  On a: <IEA=<IFA=90 => <IEA+<IFA=180 => Le quadrilatère FAEI est inscriptible, Donc d'après la théorème de Ptolémée on a: IA.EF=IE.AF+AE.IF=r.AF+r.AE Et il est connu que AF=AE (transformation de Ravi), donc: IA.EF=2r.AE =>  On a donc: \geqslant%206r%20\Leftrightarrow%20\frac{AE}{EF}+\frac{BD}{FD}%20+\frac{CE}{ED}\geqslant%203) . Et on a d'après l'IAG: ^{\frac{1}{3}}) . Donc pour montrer l'inégalité proposée, il suffit montrer que: ^{\frac{1}{3}}\geqslant%201\Leftrightarrow%20\frac{AE}{EF}\times%20\frac{BD}{FD}%20\times%20\frac{CE}{ED}%20\geq%201%20\Leftrightarrow%20AE\times%20BD\times%20CE\geq%20EF\times%20FD\times%20ED\;%20\;%20\left%20(%20*%20\right%20)) . On a d'après la formule de Héron: (p-b)(p-c)}=%20\sqrt{p%20(%20\frac{a+b+c}{2}-a%20)%20(%20\frac{a+b+c}{2}-b%20)%20(%20\frac{a+b+c}{2}-c%20)%20}=%20\sqrt{p%20(%20\frac{-a+b+c}{2})%20(%20\frac{a-b+c}{2}%20)%20(%20\frac{a+b-c}{2}%20)%20}) .  . Et on a IE=IF=ID=r, donc r est le rayon du cercle circonscrit au triangle DEF, d'où:  . En remplaçant dans (*), il vient que:  . ) . Et vu que le quadrilatère IEAF est inscriptible, on a: <EIF=180-<A => sin(<EIF)=sin(<A). De même on a: sin(<EID)=sin(<B) et sin(<FID)=sin(<C), et on a: IE=IF=ID=r. Donc il suffit montrer que: \Leftrightarrow%20S_{ABC}\geq%202r^2(\sum%20\sin%20\angle%20A)\Leftrightarrow%20S_{ABC}\geq%202r^2\times%20\frac{p}{R}\Leftrightarrow%20pr\geq%20\frac{2pr^2}{R}) . ) (d'après l'inégalité d'Euler). Et on peut vérifier facilement que l'égalité aura lieu si le triangle ABC est équilatéral. Veuillez me signaler si vous voyez une faute, Et si j'arriverai à faire le côté gauche, je vais poster ma réponse, et vous proposer un nouveau problème. | |
|
  | |
tahasinbad
Maître
 Nombre de messages : 158 Nombre de messages : 158
Age : 30
Date d'inscription : 02/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 17 Sep 2011, 21:10 Sam 17 Sep 2011, 21:10 | |
| jvoi ke c vrai mai en fait il vaut mieux utiliser la theorie de euler de geo de la relation en tre r et R ce ki est :
oi²=2R²-2Rr etant donnée ke R>=2r | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 17 Sep 2011, 21:46 Sam 17 Sep 2011, 21:46 | |
| - tahasinbad a écrit:
- jvoi ke c vrai mai en fait il vaut mieux utiliser la theorie de euler de geo de la relation en tre r et R ce ki est :
oi²=2R²-2Rr etant donnée ke R>=2r C'est une inégalité triviale, à connaître par coeur, pas besoin de la démontrer. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 23 Sep 2011, 12:57 Ven 23 Sep 2011, 12:57 | |
| Je continue donc mon travail, au premier temps, j'ai fait la substitution que j'ai déjà fait dans mon post précédant, mais j'ai pas arrivé au inégalité qu'on veut démontrer, puis j'ai pensé au sinus et les triangle rectangles, j'espère que c'est correct: On souhaite montrer que: }) . Dans le triangle AIF on a: =\frac{IF}{AI}\Longrightarrow%20\sin%20\left%20(\frac{\angle%20A}{2}%20\right%20)=\frac{r}{AI}\Longrightarrow%20AI=\frac{r}{\sin%20\left%20(\frac{\angle%20A}{2}%20\right%20)}) . De manière analogue on démontre que: }%20\;%20\;%20\mathrm{et}\;%20\;%20C%20I=\frac{r}{\sin%20\left%20(\frac{\angle%20C}{2}%20\right%20)}) . Donc l'inégalité à démontrer est équivalente à: }+\frac{r}{\sin%20\left%20(%20\frac{\angle%20A}{2}%20\right%20)}+\frac{r}{\sin%20\left%20(%20\frac{\angle%20A}{2}%20\right%20)}\leq%20\sqrt{12(R^2-Rr+r^2)}) }%20\right%20)\leq%20\sqrt{12(R^2-Rr+r^2)}\Leftrightarrow%20r^2\left%20(\sum%20\frac{1}{\sin%20\left%20(%20\frac{\angle%20A}{2}%20\right%20)}%20\right%20)^2\leq%2012(R^2-Rr+r^2)) }%20\right%20)^2\leq%2012(\frac{R^2}{r^2}-\frac{R}{r}+1)) Et on a d'après l'inégalité de CS: }%20\right%20)\geq%20\left%20(\sum%20\frac{1}{\sin%20\left%20(%20\frac{\angle%20A}{2}%20\right%20)}%20\right%20)^2) . Donc, pour montrer l'inégalité proposée, il suffit montrer que: }%20\right%20)\leq%2012(\frac{R^2}{r^2}-\frac{R}{r}+1)\Leftrightarrow%20\left%20(%20\sum%20\frac{1}{\sin%20^2%20\left%20(%20\frac{\angle%20A}{2}%20\right%20)}%20\right%20)\leq%204(\frac{R^2}{r^2}-\frac{R}{r}+1)) Et on a: -(p-b)(p-c)=p^2-pa-p^2+pb+pc-bc=p(b+c-a)-bc) -(p-b)(p-c)=\frac{1}{2}(a+b+c)(b+c-a)-bc=\frac{1}{2}((b+c)^2-a^2)-bc) -(p-b)(p-c)=\frac{1}{2}(b^2+c^2+2bc-a^2)-bc=\frac{b^2+c^2-a^2}{2}=bc.&space;\cos&space;A\;&space;\;&space;\;&space;\;&space;\mathrm{D%27apr\grave{e}s}&space;\;&space;\;&space;\mathrm{Al-Kashi}) . (1) Et on a: +(p-b)(p-c)=p^2-pa+p^2-pb-pc+bc=2p^2-p(a+b+c)+bc=2p^2-p\times&space;2p+bc=2p^2-2p^2+bc=bc) . (2) (2)-(1) => (p-c)=bc(1-\cos%20\angle%20A)\Longrightarrow%20(p-b)(p-c)=bc\left%20(%20\frac{1-\cos%20\angle%20A}{2}%20\right%20)=bc\left%20\sin%20^2%20\left%20(\frac{\angle%20A}{2}%20\right%20)%20\right) . =\sqrt{\frac{(p-b)(p-c)}{bc}}) . Et cycliquement, on montre les autres résultats. Donc il suffit montrer que: (p-c)}{bc}%20}\leq%204(\frac{R^2}{r^2}-\frac{R}{r}+1)\Leftrightarrow%20\sum%20\frac{bc}{(p-b)(p-c)}\leq%204(\frac{R^2}{r^2}-\frac{R}{r}+1)%20\Leftrightarrow%20\frac{bc(p-a)+ac(p-b)+ab(p-c)}{(p-a)(p-b)(p-c)}\leq%204(\frac{R^2}{r^2}-\frac{R}{r}+1)%20\Leftrightarrow%20bc(p-a)+ac(p-b)+ab(p-c)\leq%204(\frac{R^2}{r^2}-\frac{R}{r}+1)\left%20(%20(p-a)(p-b)(p-c)%20\right%20)) . (*) Et on a d'après la formule de Héron: (p-b)(p-c)}\Rightarrow%20pr=\sqrt{p(p-a)(p-b)(p-c)}\Rightarrow%20p^2r^2=p(p-a)(p-b)(p-c)\Rightarrow%20(p-a)(p-b)(p-c)=pr^2) . Donc: \Longleftrightarrow%20\sum%20bc(p-a)\leq%204\left%20(%20\frac{R^2}{r^2}-\frac{R}{r}%20+1\right%20)pr^2\Leftrightarrow%20p(ab+ac+bc)-3abc\leq%204\left%20(%20\frac{R^2}{r^2}-\frac{R}{r}%20+1\right%20)pr^2%20\Leftrightarrow%20p(ab+ac+bc)-12pRr\leq%204\left%20(%20\frac{R^2}{r^2}-\frac{R}{r}%20+1\right%20)pr^2%20\Leftrightarrow%20ab+ac+bc-12Rr\leq%204\left%20(%20\frac{R^2}{r^2}-\frac{R}{r}%20+1\right%20)r^2%20\Leftrightarrow%20ab+ac+bc-12Rr\leq%204\left%20(%20R^2-Rr+r^2%20\right%20)) . (**) Et on a: (p-c)(p-c)=pr^2\Rightarrow%20(p^2-pb-pc+bc)(p-c)=pr^2\Rightarrow%20p^3+p(ab+ac+bc)-p^2(a+b+c)-abc=pr^2) . -p^2\times%202p-4pRr=pr^2\Rightarrow%20ab+ac+bc=\frac{pr^2+2p^3+4pRr-p^3}{p}=r^2+2p^2+4Rr-p^2=p^2+r^2+4Rr) . Donc: \Leftrightarrow%20p^2+r^2+4Rr-12Rr\leq%204R^2-4Rr+4r^2\Leftrightarrow%20p^2+r^2-4Rr\leq%204R^2+4r^2) .  . Ce qui est juste, (l'inégalité de Gerretsen, http://www.fichier-pdf.fr/2010/12/03/geo-triangle/geo-triangle.pdf) CQFD. Problème 40: (***) Résoudre dans Z²:  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 25 Sep 2011, 15:56 Dim 25 Sep 2011, 15:56 | |
| - ali-mes a écrit:
- Problème 40: (***)
Résoudre dans Z²:  . . Je trouve que c'est facile comme exercice: Soit (x,y) un couple solution à l'équation proposée, dont l'ensemble des solutions est S. On a \Rightarrow 3^y+2\equiv2(3)) . D'autre part, on a \Rightarrow 7^x\equiv1(3)) . De ce qui précède, il résulte que S est l'ensemble vide. Sauf erreur. | |
|
  | |
judicecharatein
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 30
Date d'inscription : 19/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 25 Sep 2011, 18:12 Dim 25 Sep 2011, 18:12 | |
| | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 25 Sep 2011, 19:30 Dim 25 Sep 2011, 19:30 | |
| C'est tout aussi trivial , si x < 0 et y >0 on a un entier naturel égal à un relatif , si x>0 et y<0 alors de même si x et y < 0 on a 1/7^(-x) +1/3^(-y) < 1<2 , donc pas de solutions dans Z² .
Je vous propose celui là histoire de monté la barre un peu :
Prob (41) :
Prouvez que pour tout p premier p parmis (2p) = 2 [p^(3)] | |
|
  | |
judicecharatein
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 30
Date d'inscription : 19/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 25 Sep 2011, 21:03 Dim 25 Sep 2011, 21:03 | |
| c'est fort facile de démontrer ceci quand il s'agit de 2 modulo p mais pour 2 modulo p^3 je crois qu'il s'agit du théorème de Wolstenholme(dont je ne connais pas la démo  ) pour tout p>5 car pour p=2 p=3 et p=5 ça ne marche pas  (j'attendrais avec impatience une bonne démonstration  ) | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mer 28 Sep 2011, 17:29 Mer 28 Sep 2011, 17:29 | |
| Effectivement pour p>5 ( remarque je ne savais pas que c'est un théorème mais vu le temps que ça nous a prit avec 2 amis pour trouver je m'en doutais bien ) . Bon je met quelques indices en spoil au cas ou quelqu'un aurait le courage d'essayé : - Spoiler:
Préréquis :
ça http://fr.wikipedia.org/wiki/Identit%C3%A9_de_Vandermonde et quelques connaissances élémentaires en arithmétique .
Hints:
En appliquant la formule cité précédemment on doit démontré un autre truc et en remarquant qu'il y a une simplification par p² le résultat devient plus évident (or c'est là que ça ce corse ) ;
remarquer que ((p-1)!/(k)!(p-k)!)^2=((p-1)!/k)²[p] et le prouver , ensuite conclure en utilisant les inverses modulo
Je pense que j'y suis allez un peu fort en donnant un exo pas trivial du tout , donc libre à vous de le sauter et de proposer autre chose . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 07 Oct 2011, 16:01 Ven 07 Oct 2011, 16:01 | |
| - darkpseudo a écrit:
- C'est tout aussi trivial , si x < 0 et y >0 on a un entier naturel égal à un relatif , si x>0 et y<0 alors de même si x et y < 0 on a 1/7^(-x) +1/3^(-y) < 1<2 , donc pas de solutions dans Z² .
Je vous propose celui là histoire de monté la barre un peu :
Prob (41) :
Prouvez que pour tout p premier p parmis (2p) = 2 [p^(3)] Je ne comprends pas bien le problème que tu proposes. Merci de détailler, surtout la proposition "p parmi (2p)". | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 07 Oct 2011, 19:22 Ven 07 Oct 2011, 19:22 | |
| En attendant, je propose un exercice de ma création -dont j'ignore jusqu'à présent la solution-: Problème 42:Soit n un entier naturel. Démontrez que si p est un nombre premier supérieur à 7 et différent de 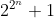 , alors \bigg)) . Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 04 Nov 2011, 15:23 Ven 04 Nov 2011, 15:23 | |
| On passe à un nouvel exercice sans perte de temps: Problème 43:Soit  et 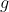 deux fonctions continues sur  tels que: :f(x)=g(x)) . Démontrez que :f(x)=g(x)) . Bonne chance. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 04 Nov 2011, 17:18 Ven 04 Nov 2011, 17:18 | |
| Salut tout le monde , j'espere que vous allez bien , je pense que ce probleme est trivial mais malgres cela , il nécéssite une petite démonstration . Le lien de l'interface Latex ne veut pas marcher donc je me contente de cela : Solution au probleme 43 Il faut tout d'abord remarquer qu' on a Quelque soit "a" appartenant a l'ensemble IR\IQ , Il existe une suite de nombre X_n appartenant a Q tel que leur limite converge vers le nombre a ( par exemple la suite de cauchy X_n+1 = X_n/2 + 1/X_n ) Donc , puisque X_n appartient a IQ , on a f(X_n)=g(X_n) puisque f et g sont deux fonctions continues sur IR donc : Lim f(X_n)=Lim f(X_n) donc f(a)=g(a) CQFD  , sauf erreur ! | |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 04 Nov 2011, 20:09 Ven 04 Nov 2011, 20:09 | |
| afin de poursuivre je propose un autre probleme,cette fois ci je pense pas qu'il est trivial... Soit P(x)=ax^3+bx ,on dit que le couple (a,b) est n-gentil si : pour tout k et m de IN : n divise P(m)-p(k) ==> n divise m-k on dit que le couple (a,b) est trés gentil si il est n-gentil pour une infinité de valeurs de n. 1) trouver un couple (a,b) qui est 51-gentil mais pas tres gentil! 2)prouver que tout les 2010-gentil sont trés gentil..  | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 04 Nov 2011, 20:40 Ven 04 Nov 2011, 20:40 | |
| Pour le problème 42 il me semble qu'il suffit de mentionner la densité de Q dans R. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 12:20 Sam 05 Nov 2011, 12:20 | |
| Bon , je vous propose ce probleme pour refaire vivre ce topic , Probleme 44 : Soit : 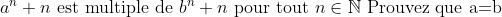 a et b appartiennent a IN
Dernière édition par Misterayyoub le Sam 05 Nov 2011, 14:37, édité 2 fois | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 12:22 Sam 05 Nov 2011, 12:22 | |
| Merci de poster les énoncés en utilisant un formulaire Latex, de préférence Codecogs, plutôt que d'héberger sur des sites de stockage d'images. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 13:00 Sam 05 Nov 2011, 13:00 | |
| Peux tu clarifier ton post momo , j'ai pas compris ce que tu veux dire ! | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 13:16 Sam 05 Nov 2011, 13:16 | |
| Tu as posté ton énoncé sur un site de stockage en ligne de photos. Ces sites ne sont pas primairement dédiés à écrire des équations mathématiques ou les stocker et vont bien souvent supprimer les fichiers après quelques mois. C'est ce qui fait que de nombreux topics sur ce forum se retrouvent sans énoncés. Comme alternative, je te conseille d'utiliser ce site pour écrire tes équations. Lorsque tu obtiens l'expression souhaitée, tu copies son adresse et tu la mets comme image ici. Ca permettra aux posts de survivre plus longtemps.   | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 14:08 Sam 05 Nov 2011, 14:08 | |
| en tout cas j'écrivais toujours sur le lien que tu viens de passer c'est juste que j'enregistrais l'image et je la postais par l'hebergement offert sur le forum , mais si ta méthode est meilleur , je vais la prendre en considération ! " target="_blank"><img src="http://latex.codecogs.com/gif.latex?Amicalement:)" title="Amicalement:)" /></a>) | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 14:19 Sam 05 Nov 2011, 14:19 | |
| Ca va tourner à un topic d'informatique mais je vois que tu as encore fait un lien vers mathsmaroc dans ton image et ça ne s'affiche pas correctement. Une fois que tu écris ton équation sur Codecogs tu obtiens un aperçu en bas au centre. Fais un clique droit dessus et copie son adresse. Ensuite sur mathsmaroc tu cliques sur le bouton pour ajouter une image et tu colles l'image. Ca donne quelque chose comme ça :  . Pour obtenir ça auparavant tu devras avoir mis : [IMAGE]http://latex.codecogs.com/gif.latex?Mathsmaroc[/IMAGE] .J'ai mis IMAGE au lieu de img pour que tu voies un peu comment c'est. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 14:24 Sam 05 Nov 2011, 14:24 | |
| ah je comprend mieux , merci infiniment ! à vos stylos maintenant :p ! | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 14:27 Sam 05 Nov 2011, 14:27 | |
| Je t'en prie. Place aux problèmes. Mets-le comme je t'ai dit stp car j'arrive pas à le voir depuis ton site. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 05 Nov 2011, 14:37 Sam 05 Nov 2011, 14:37 | |
| Done !  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 06 Nov 2011, 16:16 Dim 06 Nov 2011, 16:16 | |
| - Misterayyoub a écrit:
- Salut tout le monde , j'espere que vous allez bien , je pense que ce probleme est trivial mais malgres cela , il nécéssite une petite démonstration .
Le lien de l'interface Latex ne veut pas marcher donc je me contente de cela :
Solution au probleme 43
Il faut tout d'abord remarquer qu' on a Quelque soit "a" appartenant a l'ensemble IR\IQ , Il existe une suite de nombre X_n appartenant a Q tel que leur limite converge vers le nombre a ( par exemple la suite de cauchy X_n+1 = X_n/2 + 1/X_n )
Donc , puisque X_n appartient a IQ , on a f(X_n)=g(X_n)
puisque f et g sont deux fonctions continues sur IR donc :
Lim f(X_n)=Lim f(X_n)
donc f(a)=g(a)
CQFD  , sauf erreur ! , sauf erreur ! J'ai proposé l'exercice, et j'ai oublié de mentionner qu'il faut le traiter à l'aide de la définition épsilonienne de la continuité. C'est bien ... - rimele a écrit:
- afin de poursuivre je propose un autre probleme,cette fois ci je pense pas qu'il est trivial...
Soit P(x)=ax^3+bx ,on dit que le couple (a,b) est n-gentil si :
pour tout k et m de IN : n divise P(m)-p(k) ==> n divise m-k
on dit que le couple (a,b) est trés gentil si il est n-gentil pour une infinité de valeurs de n.
1) trouver un couple (a,b) qui est 51-gentil mais pas tres gentil!
2)prouver que tout les 2010-gentil sont trés gentil..  Il s'agit du problème 45. Merci de le renuméroter afin d'être traité. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  | |
| |
|
  | |
| | Préparations aux olympiades de Terminale (2012) |  |
|
