| | Préparations aux olympiades de Terminale (2012) |  |
|
+23rimele judicecharatein mohamed diai yasserito tahasinbad the kiler darkpseudo Incompri M.Marjani boubou math samsoum05 kaj mima manazerty Misterayyoub nmo mr.mertasayeker az360 expert_run xyzakaria Othmaann ali-mes n.naoufal Mehdi.O 27 participants |
|
| Auteur | Message |
|---|
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 05 Sep 2011, 20:26 Lun 05 Sep 2011, 20:26 | |
| SOLUTION DU PROBLEME 33
Notons R le rayon du cercle circonscrit du triangle ABC évidemment R=1
D'abord , on a par la formule d'Euler 2r=<R=1 ---> r=<1/2 ---> 1/3(1+r)²=<3/4--->
1-1/3(1+r)²>=1/4
donc pour prouver l’inégalité souhaité il suffit de montrer que p=<1/4 .
Notons R_1 le rayon du cercle circonscrit du triangle A'B'C', encore en utilisant le formule d'Euler p=<1/2R_1 .
d'une autre part, par le théorème des neufs point on a R_1=1/2R ---> p=<1/4R---> p=<1/4
CQFD
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 05 Sep 2011, 20:33 Lun 05 Sep 2011, 20:33 | |
| - boubou math a écrit:
- SOLUTION DU PROBLEME 33
Notons R le rayon du cercle circonscrit du triangle ABC évidemment R=1
D'abord , on a par la formule d'Euler 2r=<R=1 ---> r=<1/2 ---> 1/3(1+r)²=<3/4--->
1-1/3(1+r)²>=1/4
donc pour prouver l’inégalité souhaité il suffit de montrer que p=<1/4 .
Notons R_1 le rayon du cercle circonscrit du triangle A'B'C', encore en utilisant le formule d'Euler p=<1/2R_1 .
d'une autre part, par le théorème des neufs point on a R_1=1/2R ---> p=<1/4R---> p=<1/4
CQFD
C'est Faux ! | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 | |
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 05 Sep 2011, 21:01 Lun 05 Sep 2011, 21:01 | |
| - boubou math a écrit:
- Mehdi.O a écrit:
- boubou math a écrit:
- SOLUTION DU PROBLEME 33
Notons R le rayon du cercle circonscrit du triangle ABC évidemment R=1
D'abord , on a par la formule d'Euler 2r=<R=1 ---> r=<1/2 ---> 1/3(1+r)²=<3/4--->
1-1/3(1+r)²>=1/4
donc pour prouver l’inégalité souhaité il suffit de montrer que p=<1/4 .
Notons R_1 le rayon du cercle circonscrit du triangle A'B'C', encore en utilisant le formule d'Euler p=<1/2R_1 .
d'une autre part, par le théorème des neufs point on a R_1=1/2R ---> p=<1/4R---> p=<1/4
CQFD
C'est Faux !  Oui je m'excuse je me suis un peu précipité, je ne conaissais pas ce théorème avant  . A toi de proposer un nouveau probleme. | |
|
  | |
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 05 Sep 2011, 21:24 Lun 05 Sep 2011, 21:24 | |
| solution du prob 33
soit R' le rayon du cercle circonscrit au triangle A'B'C'
donc R'=1/2
on note x=<BAC ; y=<ABC et z=<ACB
donc <B'A'C'=180-2x ; <A'B'C'=180-2y et <A'C'B'=180-2z
tout d'abord on a r/R=cosx + cosy + cosz - 1 <=> r+1=cosx + cosy + cosz
et de meme p/R'= -cos2x -cos2y -cos2z -1=2-2(cos²x+cos²y+cos²z)
par suite 1-p=cos²x+cos²y+cos²z
l'inegalité à demontré est equivalente à 3(cos²x+cos²y+cos²z)>=(cosx + cosy + cosz)² ce qui est vraiment clair | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 05 Sep 2011, 21:27 Lun 05 Sep 2011, 21:27 | |
| Je n'ai pas d'exercice a poster donc je laisse la main à quelqu'un d'autre  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 05 Sep 2011, 21:56 Lun 05 Sep 2011, 21:56 | |
| Problème 34:Résoudre dans IR le système suivant :  | |
|
  | |
tahasinbad
Maître
 Nombre de messages : 158 Nombre de messages : 158
Age : 30
Date d'inscription : 02/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 13 Sep 2011, 19:23 Mar 13 Sep 2011, 19:23 | |
| peu etre c tré expert celui la comme exoo , jcroi avoir un exo normale :
soit a,b,c des longueurs d'un triangle .
Prouvez que
(a/b+c)+(b/a+c)+(c/a+b) <2 j'attends des interventions! | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 13 Sep 2011, 19:35 Mar 13 Sep 2011, 19:35 | |
| - tahasinbad a écrit:
- peu etre c tré expert celui la comme exoo , jcroi avoir un exo normale :
soit a,b,c des longueurs d'un triangle .
Prouvez que
(a/b+c)+(b/a+c)+(c/a+b) <2 j'attends des interventions! C'est un exercice connu ...suffit de diviser le tout par 2 et utilise l'inegalite geometrique a+b>c pr avoir a/2(b+c) +b/2(a+c) +c/2(a+b)<a/a+b+c +b/a+b+c +c/a+b+c=1 sauf erreur. | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 13 Sep 2011, 20:39 Mar 13 Sep 2011, 20:39 | |
| si vous voulez, voici un problème 36:a,b,c des réels positifs, Montrer que: }{\sqrt{(a+b)(b+c)(c+a)}})
Dernière édition par kaj mima le Mer 14 Sep 2011, 16:48, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 13 Sep 2011, 21:27 Mar 13 Sep 2011, 21:27 | |
| - tahasinbad a écrit:
- peu etre c tré expert celui la comme exoo , jcroi avoir un exo normale :
soit a,b,c des longueurs d'un triangle .
Prouvez que
(a/b+c)+(b/a+c)+(c/a+b) <2 j'attends des interventions! On pourrait dire qu'il est un peu moche , c'est tous . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mer 14 Sep 2011, 16:22 Mer 14 Sep 2011, 16:22 | |
| - expert_run a écrit:
- Problème 34:
Résoudre dans IR le système suivant :
 Est ce que tu veux dire  ou 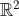 ? La question se pose automatiquement car on a deux lignes dans le système. De plus, il faut qu'on ait deux inconnues pour pouvoir résoudre ce problème. Cela n'est pas le cas, car on dispose de deux équations et de trois inconnus: je pense qu'on ne peut pas trouver les solutions. Merci de proposer une solution et de répondre à mes questions. | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mer 14 Sep 2011, 21:19 Mer 14 Sep 2011, 21:19 | |
| | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mer 14 Sep 2011, 22:46 Mer 14 Sep 2011, 22:46 | |
| Solution pour 36:L’inégalité est équivalente à : \sqrt{(a+b)(c+a)}}{a}+\frac{(a+c)\sqrt{(b+c)(a+b)}}{b}+\frac{(a+b)\sqrt{(b+c)(a+c)}}{c}\geq&space;4(a+b+c)) On a: (c+a)}\underset{C.S}{\geq&space;}a+\sqrt{bc}) Donc : \sqrt{(a+b)(c+a)}}{a}+\frac{(a+c)\sqrt{(b+c)(a+b)}}{b}+\frac{(a+b)\sqrt{(b+c)(a+c)}}{c}\geq&space;2(a+b+c)+\frac{(b+c)(\sqrt{bc})}{a}+\frac{(a+c)(\sqrt{ac})}{b}+\frac{(a+b)(\sqrt{ab})}{c}\geq&space;2(a+b+c)+2(\frac{bc}{a}+\frac{ac}{b}+\frac{ab}{c})) On suppose que a >=b>=c Donc  Alors: \sqrt{(a+b)(c+a)}}{a}+\frac{(a+c)\sqrt{(b+c)(a+b)}}{b}+\frac{(a+b)\sqrt{(b+c)(a+c)}}{c}\geq&space;2(a+b+c)+\frac{(b+c)(\sqrt{bc})}{a}+\frac{(a+c)(\sqrt{ac})}{b}+\frac{(a+b)(\sqrt{ab})}{c}\geq&space;4(a+b+c)) | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 15 Sep 2011, 00:16 Jeu 15 Sep 2011, 00:16 | |
| Il y a une erreur dans le problème 34 je suis désolé . | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 15 Sep 2011, 00:17 Jeu 15 Sep 2011, 00:17 | |
| Probleme 37 :
a,b,c>0 tel que : a²+b²+c²=1 . Montrer que : a+b+c+1/(abc) >= 4sqrt(3) . | |
|
  | |
mohamed diai
Maître
 Nombre de messages : 113 Nombre de messages : 113
Age : 30
Localisation : meknes
Date d'inscription : 17/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 15 Sep 2011, 15:07 Jeu 15 Sep 2011, 15:07 | |
| notons que: 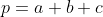 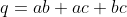 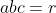 on sait que  alors  et comme  alors  et comme  le résultat en découle. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 15 Sep 2011, 17:14 Jeu 15 Sep 2011, 17:14 | |
| Dans la troisième ligne l'équivalence est fausse il faut juste dire qu'il suffit de prouver que
p+ (9/(pq))>= 4sqrt(3) | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 15 Sep 2011, 21:41 Jeu 15 Sep 2011, 21:41 | |
| probleme 38 (OWn facile) :x,y,z>0 tel que : xyz>=x+y+z Montrer que : (x+z)}\geq%20\frac{9}{\sum%20x^2(x^2+1)}) | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 16 Sep 2011, 12:43 Ven 16 Sep 2011, 12:43 | |
|
Dernière édition par expert_run le Ven 16 Sep 2011, 13:25, édité 1 fois | |
|
  | |
mohamed diai
Maître
 Nombre de messages : 113 Nombre de messages : 113
Age : 30
Localisation : meknes
Date d'inscription : 17/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 16 Sep 2011, 12:48 Ven 16 Sep 2011, 12:48 | |
| - expert_run a écrit:
- Dans la troisième ligne l'équivalence est fausse il faut juste dire qu'il suffit de prouver que
p+ (9/(pq))>= 4sqrt(3) dsl vous avez raison  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 16 Sep 2011, 19:34 Ven 16 Sep 2011, 19:34 | |
| a propose de P38 :je poste ma solution demain inchalah si quelqu'un n'a trouver !!  (pour ne pas stopper le marathon !!!) essayer C'est très facile . | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 16 Sep 2011, 21:02 Ven 16 Sep 2011, 21:02 | |
| Solution du problème 38:On a selon Cauchy: (x+z)}\geq&space;\frac{9}{\sum_{cyc}(x^{2}+xz+xy+yz)}) Donc il faut démontrer que: \leq&space;\sum_{cyc}x^{2}(x^{2}+1)&space;) Ce qui est équivalent à:  On sait que: ^{2}\geq&space;3\sum_{cyc}xy&space;) et que, selon Cauchy: ^{2}) Donc, il reste à prouver que:  ce qui est équivalent à :  On a selon AM-GM: x^4+y^4+z^4 >= 3 (xyz)^(4/3) Et selon la condition: xyz>=x+y+z>=3(xyz)^(1/3) ce qui donne: xyz>=V27 , d'où la conclusion. Sauf erreur! | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 17 Sep 2011, 16:20 Sam 17 Sep 2011, 16:20 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 17 Sep 2011, 17:15 Sam 17 Sep 2011, 17:15 | |
| Je propose un nouveau problème: Problème 39:Soit ABC un triangle, et I le centre de son cercle inscrit. Soit R et r les rayons respectifs des cercles circonscrit et inscrit au triangle ABC. Démontrez l'inégalité suivante: }\ge AI+BI+CI\ge6r) . Bonne chance. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  | |
| |
|
  | |
| | Préparations aux olympiades de Terminale (2012) |  |
|
