Préparation aux olympiades.

L-W-P a toi de proposer un exeecice ! Géométrie si possible..

exo 51
Soit ABC un triangle est un point D a l’intérieur de celui-ci tel que : <DAC=<DCA=30 et <DBA=60 . soit E le milieu de [BC] . F un point de AC tel que : AF=2FC . Prouver que (DE) et (EF) sont perpendiculaire .

On peut seulement démonter que <DEF = <DGF =90° en cour de réfléchir ...

Proposition de ;Ahmed Taha (bis)

Amiral ! A vous de proposer un exercice de géométrie si possible !

Comme AMIRAL n'a pa poste d'exercice , je propose cet exercice de geometrie . Soit ABCD un parallelograme tel que l'angle A est aigu. Le cercle de diamètre AC rencontre les droites BC et CD en E et F respectivement. La tangente au cercle en point A coupe BD en P. Montrez que les trois points P,F,E sont alignes.

J'Ajoute un autre exercice afin d'Accelerer le jeu
Trouver toutes les fonctions definies de R vers R* qui verifient f(x²-y²)=xf(x)-yf(y)

Personne ! -____________-'''

Je ne peux pas voir l'exercice :p

Je vous rappelle qu'il y a un autre exercice de geometrie en plus de l'EF

bianco verde a écrit:

J'Ajoute un autre exercice afin d'Accelerer le jeu
Trouver toutes les fonctions definies de R vers R* qui verifient   f(x²-y²)=xf(x)-yf(y)

posons P(x,y)=>f(x²-y²)=xf(x)-yf(y)

P(x,0)=>f(x²)=xf(x) et P(0,x)=> f(-x²)=-xf(x)=-f(x²)

alors f est impaire et f(x²-y²)=f(x²)-f(y²)=f(x²-y²)=> f(x-y)=f(x)-f(y) pr tt x,y>0 (1)

prend x=a,y=-b dans (1) avec a>0 et b<0 donc f(a+b)=f(a)+f(b) pr tt a>0 et b<0 *

prend x=a+b,y=b dans (1) avec a,b>0 donc f(a+b)=f(a)+f(b) pr tt a,b>0**

prend x=-a,y=-a-b dans (1) avec a,b<0 donc f(a+b)=f(a)+f(b) pr tt a,b<0 ***

prend x=-a,y=b dans (1) avec a,b<0 donc f(a+b)=f(a)+f(b) pr tt a<0 et b<0 ****

après les 4 résultats *,**,******* on a : f(x+y)=f(x)+f(y) pr tt x,y£IR  (EF de Caushy) donc f(x)=ax pr tt a£IR.
réciproquement cette solution est vrai.

OUI , vous pouvez proposer un exo

bianco verde a écrit:

OUI , vous pouvez proposer un exo

je pense que l'exo de geo n'ai pas encore résolue

malgré ça je propose ce probleme :

Trouver toutes les fonctions surjectives 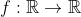telles que 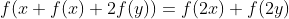pour tout .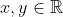

j'ai déjà postée une solution incomplète ici

.

bianco verde a écrit:

Soit ABCD un parallelograme tel que l'angle A est aigu. Le cercle de diamètre AC rencontre les droites BC et CD en E et F respectivement. La tangente au cercle en point A coupe BD en P. Montrez que les trois points P,F,E sont alignes.

bianco verde a écrit:

Indice pour l'exo de geo :p

Indice:

oui on peut utiliser l'un des deux théor Ceva ou Menelaüs pour résoudre le problème.
pour moi j'ai fait une autre méthode :

Théorèmes :

Montrons que XEFG est inscriptible :

Montrons que XGHI est inscriptible:

Conclusion :
les quadrilatères XEFG,XGHI et EFHI sont inscriptibles alors les droites (XG),(IH) et (EF) sont concourantes (d’après le théorème 1).
et puisque donc d'où P,F,E sont alignés.