| | Préparation aux olympiades. |  |
|
+10elmrini Sketshup mae24 Zouhair-Evariste legend-crush elidrissi aymanemaysae L-W-P aminesm bianco verde 14 participants |
|
| Auteur | Message |
|---|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Ven 07 Mar 2014, 20:22 Ven 07 Mar 2014, 20:22 | |
| - signe:
Bézout  en mq que PGCD(21n+3;14n+2)=1
| |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Ven 07 Mar 2014, 20:45 Ven 07 Mar 2014, 20:45 | |
| Bonsoir.
On a pour n appartenant à IN*, 21n+3 =3(7n+1) et 14n+2=2(7n+1), donc 7n+1 est le PGCD de (21n+3) et (14n+2), avec 7n+1 supérieur ou égal à 8, donc (21n+3)\(14n+2) est réductible.
Pour n=0 on a (21n+3)\(14n+2)=3\2 fraction irréductible.
L'énoncé de l'exercice aurait dû être: pour n appartenant à IN*, montrer que (21n+3)\(14n+2) est réductible.
L'exercice 11 est très interessant, Merci M. ElIdrissi pour m'avoir orienté vers ce genre d'exercice. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Ven 07 Mar 2014, 21:40 Ven 07 Mar 2014, 21:40 | |
| L'exercice est en fait montrer que 21n+4/14n+3 est irrecductible, ce qui est résolvable usant de Bezout. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Ven 07 Mar 2014, 21:53 Ven 07 Mar 2014, 21:53 | |
| si l'exercice est pour (21n+4)/(14n+3), on a :
3*(14n+3) - 2*(21n+4) = 42n+9-42n+8=1, donc par le théorème de Bezout , 14n+3 et 21n+4 sont premiers entre eux, donc (21n+4)/(14n+3) est irréductible.
Pour animer le sujet, je propose de montrer que: 10001^10001 + 10001^401 est un carré parfait. | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Ven 07 Mar 2014, 22:16 Ven 07 Mar 2014, 22:16 | |
| desolé, vous avez raison. faute de frappe. Mr aymane je vais travailler sur votre "colosse aux pieds d argil" comme vos l appellez | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 09:05 Sam 08 Mar 2014, 09:05 | |
| Je rappelle qu'il y a toujours un exercice non résolu.
EXO.7 TROUVER TOUS LES POLYNOMES TELS QUE P(1)=2 ; P(2)=4 ; P(4)=7 ; P(6)=8 . | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 10:49 Sam 08 Mar 2014, 10:49 | |
| - aymanemaysae a écrit:
- si l'exercice est pour (21n+4)/(14n+3), on a :
Pour animer le sujet, je propose de montrer que: 10001^10001 + 10001^401 est un carré parfait. 10001^10001 + 10001^401 = 1+1=2 [10] il nest donc pas un carré parfait. sauf erreur. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 11:16 Sam 08 Mar 2014, 11:16 | |
| En ce qui concerne l'exercice 7, il faut préciser de quels polynômes on parle: je présume qu'il s'agit des élèments de IR[X], n'est ce pas? De plus, je crois qu'il faut préciser le degré minimal des polynômes en question, car on peut à la main tracer des courbes à volonté qui passent par les quatres points (1;2), (2;4), (4;7) et (6,  . | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 11:24 Sam 08 Mar 2014, 11:24 | |
| je crois que polynome est de degré 3 . sinon il yen aurait infiniment
si c est le cas, on utilise ll'interpolation lagrangienne tout simplement ^^ | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 11:27 Sam 08 Mar 2014, 11:27 | |
| Désolé, mais c'est un carré parfait, et ce n'est qu'un cas particulier d'un problème plus général.
Le problème utilise une astuce très simple: malgré la présence de grands nombres, il est simple à résoudre par une simple identité remarquable, c'est pour cette raison qu'il ressemble au colosse aux pieds d'argile de la mythologie grecque. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 11:40 Sam 08 Mar 2014, 11:40 | |
| Je suis tout à fait d'accord avec vous, M. Elidrissi, mais j'aimerai attendre la confirmation de M. BIANCO_VERDE. | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 11:52 Sam 08 Mar 2014, 11:52 | |
| si c est un carréparfait il devrait etre egal a 1, 4, 5,6,9 ou 0 modulo 10 , comme il est egal a 2 modulo 10 il ne peut pas etre un carré parfait....
sauf erreur
s'il ya une erreur dans mon raisonnement je vous prie de me la signaler | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 12:14 Sam 08 Mar 2014, 12:14 | |
| Pour l'exercice 7, et sauf erreur, le polynôme minimal qui est de degré 3, obtenu par la méthode d'interpolation Lagrangienne est: P(x) = 1/180 x^3 - 1927/180 x^2 + 32/15 x +7/5 .
Si c'est pas trop demandé, j'aimerai avoir une confirmation.
Merci. | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 12:18 Sam 08 Mar 2014, 12:18 | |
| p(1)=1/180 + 1927/180 + 32/15 + 7/5 =12,24444.... | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 12:20 Sam 08 Mar 2014, 12:20 | |
| A l'attention de M. Elidrissi, et pour voir si je n'ai pas commis de fautes, j'édite ma solution en lui demandant de la corriger si nécessaire: j'attendrai bien sur une confirmation ou une infirmation de votre part, ou de la part de M. BIANCO_VERDE. Merci.  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 12:25 Sam 08 Mar 2014, 12:25 | |
| c'est correct, du coup il s ecrit sous la forme de 2 carrés parfaits, et n'est pas un carré parfait
votre ennoncé etait donc erronné ^^ | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 12:52 Sam 08 Mar 2014, 12:52 | |
| Vous avez raison, il fallait écrire "sous forme de deux carrés parfaits".
Je m'excuse pour le dérangement que cette erreur dans l'enoncé a causé. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 13:18 Sam 08 Mar 2014, 13:18 | |
| Pour l'exercice 7, je rectifie ma proposition, et j'avance que le polynôme minimal qui est de degré 3, obtenu par la méthode d'interpolation Lagrangienne est: P(x) = -1/60 x^3 - 1/20 x^2 + 34/15 x - 1/5 .
J'ai suivi votre méthode pour m'assurer de l'exactitude de ma démarche en calculant P(1), P(2), P(4) et P(6), mais ça n'empêche pas que j'attendrai votre confirmation pour m'assurer que je n'ai pas fait de fautes de calcul.
Merci. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 13:30 Sam 08 Mar 2014, 13:30 | |
| En ce qui concerne toujours, l'exercice n° 7, jaimerai ajouter que les polynômes de Lagrange que j'ai trouvés sont: L0(x) = -1/15 (x^3 -12 x^2 + 44 x - 48) L1(x) = 1/8 (x^3 -11 x^2 + 34 x - 24) L2(x) = -1/12 (x^3 - 9 x^2 + 20 x - 12) L3(x) = 1/5 (x^3 -7 x^2 + 14 x - 8)  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 14:51 Sam 08 Mar 2014, 14:51 | |
| pas de problemes Mr.aymanemaysae .
le polynome est donc correct ^^
a vous de poster | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 14:59 Sam 08 Mar 2014, 14:59 | |
| Pour mettre fin au "Silence" qui règne, je propose ce problème: 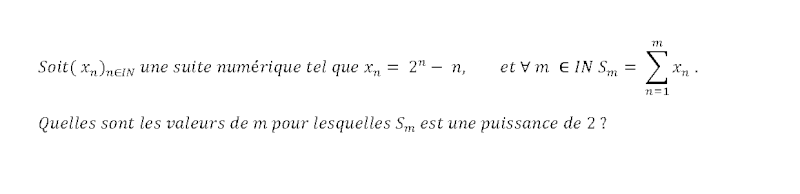 | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 15:22 Sam 08 Mar 2014, 15:22 | |
| Desolé pour le retard mr aymanemaysae .. quant a l exercice des polynômes c est le fait qu aucune indication sur le degre n a été donnée qui me laisse bloqué...
Et pour l exercice que vs avez poster je doute qu'il soit du niveau du tronc commun. Donc je vous prie de poser un exercice du genre qui peut poser des problèmes lors de l' épreuve ( qu'on passera le vendred incha Allah) | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 17:26 Sam 08 Mar 2014, 17:26 | |
| Pour le plaisir, et sans vouloir semer la désordre dans cette page: c'est seulement parce que j'ai bien aimé l'exercice que M. Elidirissi avait proposé: EXERCCE 11montrer que pour tout a b et c strictement positifs, on a PGCD(a,b,c)^2/(PGCD(a,b).PGCD(a,c).PGCD(b,c))= PPCM(a,b,c)^2/(PPCM(a,b).(PPCM(a,c).PPCM(b,c))Je veux seulement votre avis sur la démarche que j'ai suivie pour le résoudre, et si M. Elidrissi le veut bien, j'aimerai bien qu' il le corrige et me fasse l'honneur de m'indiquer les erreurs que j'ai commises.   | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 17:39 Sam 08 Mar 2014, 17:39 | |
| Exercice alternatif à l'exercice sus mentionné sur les sommes:
Soient a, b, c et d des réels tels que a^2 + b^2 + c^2 + d^2 = 4, montrer que :
a^3 + b^3 + c^3 + d^3 =< 8 .
Si quelqu'un veut comparer sa solution de l'exercice sur les sommes, je suis prêt d'être de la partie. | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  Sam 08 Mar 2014, 18:03 Sam 08 Mar 2014, 18:03 | |
| Il s'agit de la premiere ineq dans le livre du grand VASILE CIRTOAJE. on a sum a^2 =4 donc a^2<4 <--->a<2 DONC a-2 <0 d'ou a^2 (a-2)<0 <--->a^3 <2a^2 de la mm facon b^3 <2b^3 :et c^3<2c^2 ET d^3 <2d^2 En sommant : on trouve a^3 +b^3+c^3+d^3 <2(a^2+b^2+c^2+d^2)=8 D'ou le resultat voulu JE TIENS A VOUS REMERCIER POUR LES EXERCICES ASTUCIEUX QUE VOUS POSTEZ  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation aux olympiades. Sujet: Re: Préparation aux olympiades.  | |
| |
|
  | |
| | Préparation aux olympiades. |  |
|
