Préparations aux olympiades de Terminale (2012)

Mehdi.O a écrit:

Solution au problème 18:
Remarquer d'abord que 2009=49.41 et puisque pgcd(49,41)=1 alors il suffit de prouver que 49|A=20^{n}+15^{n}+8^{n}6^{n} et 41|A.
- Travaillons modulo 41 :
Tout d'abord la condition que n est un entier qui finit par le chiffre 5, veut dire que n est multiple de 5 mais pas de 10, soit il s'écrit sous la forme : n=5k=5(2k'+1)=10k'+5.
Nous avons : 20^{n}=20^{5k}=(20^{5})^{k} =(32)^{k}(mod 41)
De même on trouve 15^{n}=(14)^{k}(mod 41) et 8^{n}=(9)^{k} (mod 41) et 6^{n}=(27)^{k}(mod 41).
Ainsi A = ((32)^{k}+(9)^{k})+((14)^{k}+(27)^{k})=0(mod 41) ( puisque 32+9=41 et 14+27=41 et puisque k est impaire donc on obtient la facotrisation a^{k}+b^{k}=(a+b)(...))
Ainsi 41|A
Et on procédant de la même façon on trouve que 49|A
Ainsi 2009=49.41|A

je vois que c'est juste ... tu peut poster un prob.

Puisque Mehdi.O n'a rien poster. Je poste ce problème.
Problème 19:
Comment doit-on répartir n boules dans K boites de façon à minimiser le nombre de paires de boules qui appartiennent à une même boite?

je crois que ce problème est sur animath ,dans le cours des inégos

Mehdi.O a écrit:

M.Marjani a écrit:

az360 a écrit:

Solution Au Problème 17 :

Spoiler:

Fermat s'applique sous la condition: p se différe de a dans la formule a^{p-1}-1=0[p] .

Ce n'est pas Fermat mais juste de simples congruences modulo 5. Tu peux vérifier cela facilement en classe d'équivalence modulo 5 dans Z/5Z ( en excluant bien sûr 0 modulo 5 vu que p est premier )

Je vois que c'est bien le petit théorème de Fermat:
On a 5 premier, et p entier non divisible par 5 - puisque p est premier et p>5 - , alors : p^4 ≡ 1 [5]

kaj mima a écrit:

Mehdi.O a écrit:

M.Marjani a écrit:

az360 a écrit:

Solution Au Problème 17 :

Spoiler:

Fermat s'applique sous la condition: p se différe de a dans la formule a^{p-1}-1=0[p] .

Ce n'est pas Fermat mais juste de simples congruences modulo 5. Tu peux vérifier cela facilement en classe d'équivalence modulo 5 dans Z/5Z ( en excluant bien sûr 0 modulo 5 vu que p est premier )

Je vois que c'est bien le petit théorème de Fermat:
On a 5 premier, et p entier non divisible par 5 - puisque p est premier et p>5 - , alors : p^4 ≡ 1 [5]

Oui, je n'ai pas dit que Fermat ne s'applique, juste qu'il y a une autre méthode avec les congruences

nmo a écrit:

Exercice 5:
Soit a, b, c, d, e, et f six nombres entiers naturels différents deux à deux.
On pose S=a+b+c+d+e+f, P=ab+bc+ca-de-ef-fd et R=abc+def.
On suppose que S divise les deux nombres P et R.
Démontrez que S ne peut pas être un nombre premier.

Voici le travail que j'ai fait:
On a: et .
De plus, on a:
.
On peut donc conjecturer que: .
En effet, soit n un entier quelquonque, on a:
.
Et ainsi, il s'ensuit que:
.
Il résulte que: .
Et voici la suite (qui n'est pas propre à moi):
On suppose maintenat par l'absurde que S est prmier, et on prends .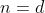
Donc .
Et puisque S est premier, on aura forcément: .
Ce qui est impossible, car on a: .
Ainsi, ce qu'on a supposé s'avère faux.
Et par conséquent S n'est pas premier.
CQFD.
Sauf erreur.

Je propose une inégalité qui n'est plus facile à démontrer:
Problème 20:
Soient a, b et c des rééls strictement positifs tels que .
Démontrez que: .
Bonne chance.

salut!
vu que le problème 20 n'est toujours pas résolu,alors je propose un nouveau problème:
problème 21
soient a,b,c des rééls positifs
MQ:
(a²+2)(b²+2)(c²+2)>=9(ab+bc+ca)

nmo a écrit:

Problème 20:
Soient a, b et c des rééls strictement positifs tels que .
Démontrez que: .
Bonne chance.

Je donne une solution:
Soient a,b et c des rééls strictement positifs.
On a l'inégalité: .
En effet, on a:
.
On a selon l'inégalité arithmético-géométrique:
-, soit .==>(1)
-, soit .==>(2)
-, soit .==>(3)
En sommant ces inégalités, on trouve que .
Ce qui est demandé.
Ainsi, on a démontré que .
De même, on démontre que et .
En sommant ces inégalités, on aura .
Soit .==>(4)
Et puisque , il vient soit .==>(5)
De 4 et 5, on touve que .
On s'intéresse maintenant au cas d'égalité:
Selon les inégalités 1, 2 et 3, l'égalité aura lieu si et seulement si ,
et c'est à dire .
Ainsi le seul cas d'égalité est lorsque .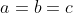
Ce qui achève la démonstration.
Sauf erreur.

manazerty a écrit:

salut!
vu que le problème 20 n'est toujours pas résolu,alors je propose un nouveau problème:
problème 21
soient a,b,c des rééls positifs
MQ:
(a²+2)(b²+2)(c²+2)>=9(ab+bc+ca)

On démontre premièrement le lemme suivant:
soient a,b et c trois rééls strictement positifs.
On a l'inégalité: .
On pose 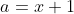, 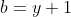et .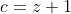
On a donc:
.
On distingue maintenant deux cas:
-Cas premier: , soit .
Et on a aussi .
Soit en résumé .
Avec égalité si et seulement si .
-Cas second: , soit .
Donc l'un des rééls x, y ou z est négatif.
On prends . (les autres cas se traitent d'une manière analogue).
Il s'ensuit que .
On a .
On sait que a est positif, donc .
Et puisque 2yz est positif, il vient que .
Et on a aussi .
Soit en résumé .
Ce qui équivaut à .
Avec égalité si et seulement si .
-Conclusion:
Dans tous les cas: .
Avec égalité si et seulement si .
Donc .
Avec égalité si et seulement si .
C'est à dire lorsque .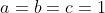

Maintenant, on revient à l'exercice proposé:
On simplifie le côté gauche de l'inégalité:
.
On a selon l'inégalité arithmético-géométrique: .
Avec égalité si et seulemnt si abc=1.
Donc .
Et on a selon lemme démontré: .
Il résulte que: .==>(1)
Avec égalité si et seulement si: .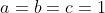
On a selon l'inégalité de Cauchy Schwartz: .
Avec égalité si et seulement si .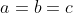
Donc soit .
Il résulte que: .==>(2)
On utilise l'inégalité arithmético-géométrique pour trouver que:
-, avec égalité si et seulement si ab=1.
-, avec égalité si et seulement si bc=1.
-, avec égalité si et seulement si ca=1.
En sommant ces inégalité membre par membre, on aura: .
Donc .
Il résulte que: .==>(3)
En sommant les inégalités 1, 2 et 3 membre par membre, on aura: .
Donc .
Ce qui s'écrit encore .
Le cas d'égalité est lorsque: abc=1, ab=1, bc=1, ca=1 et a=b=c.
C'est à dire lorsque a=b=c=1.
CQFD.
Sauf erreur.

formidable! on peut également utiliser une substitution trigonométrique :
a=sqrt(2)tgA et b=sqrt(2)tgB et c=sqrt(2)tgC
avec A,B,C E (0,pi/2)
je posterai la solution plus tard..(ps: ce n'est pas ma propre solution!)

Je présente ma solution au problème 21, qui est différente de celle de nmo :
Solution au problème 21:
L'inégalité est équivalente après dévellopemment à :
.
On pose : p=a+b+c et q=ab+ac+bc et r=abc.
Alors l'inégalité devient équivalente à :
.
-Cas 1: .
Alors, q^3>=27r^2>=5832 et ainsi q>=18.
Mais puisque f(p)=(2p-r)² +2(q-8 )(q-1/2)>=0.
Et Ce qui est vrai.
Alors on a fini avec ce cas.
-Cas 2:
Dès lors nous avons : .
Mais par I.A.G : 2p>=6(r)^(1/3)>=r ainsi f'(p)>0, ce qui donne f est strictement croissante.
Et puisque p²>=3q et p^3>=27r alors p est minimal lorsque a=b=c en d'autres termes lorsque p^6=27q^3=729r^2.
Ainsi en posant x=(r)^(1/3) On obtient : f(p)>=x^6+6x^4-15x²+8>=0 ce qui est vrai vu que c'est équivalent à :
(x²-1)²(x²+8 )>=0
Et ainsi on a fini avec ce cas aussi.
En conclusion nous avons pour tout a,b,c >0 l'inégalité suivante :
(a²+2)(b²+2)(c²+2)>=9(ab+ac+bc).

Je propose un nouvel exercice:
Problème 22:
Soit (C) un cercle de centre O.
Soit [AB] une corde de (C), et I le milieu de [AB]. [MN] est une autre corde ce (C) passant par I.
Les tangentes à (C) en M et N coupent (AB) en deux points noté P et Q respectivement.
Montrez que AP=BQ.
Bonne chance.

Solution au problème 22:

Sans nuire à la généralité du problème on suppose que O se trouve à l'intérieur de l'angle{PMI} et O se trouve à l'extérieur de l'angle{QNI}.
Puisque I est le milieu de AB et le triangle AOB est isocèle donc OI est perpendiculaire à AB, d'autre part puisque la droite MP est tangente à (C) alors angle{PMO}=90 et de même on obtient angle{QNO}=90 et ainsi les deux quadrilatères QION et MIOP sont inscirptibles, ce qui donne : angle{QPO}=angle{IPO}=angle{OMI}=angle{ONI}=angle{OQI}=angle{OQP}, et ainsi le triangle POQ est isocèle ce qui veut dire que IP=IQ i.e : AP=BQ.

Mehdi.O a écrit:

Solution au problème 22:
Sans nuire à la généralité du problème on suppose que O se trouve à l'intérieur de l'angle{PMI} et O se trouve à l'extérieur de l'angle{QNI}.
Puisque I est le milieu de AB et le triangle AOB est isocèle donc OI est perpendiculaire à AB, d'autre part puisque la droite MP est tangente à (C) alors angle{PMO}=90 et de même on obtient angle{QNO}=90 et ainsi les deux quadrilatères QION et MIOP sont inscirptibles, ce qui donne : angle{QPO}=angle{IPO}=angle{OMI}=angle{ONI}=angle{OQI}=angle{OQP}, et ainsi le triangle POQ est isocèle ce qui veut dire que IP=IQ i.e : AP=BQ.

Très bien. Une solution rapide et efficace.
A toi de proposer un nouvel exercice.

Voici un problème de géométrie assez facile mais délicieux à résoudre.
Problème 23:
Soit ABC un triangle dont les angles sont aigus. Le cercle inscrit de ABC touche BC,AC, et AB en D,E et F respectivement. La bissectrice de angle{BAC} coupe DE et DF en K et L respectivement. Et soit A_1 un point tel que AA_1 est une hauteur du triangle ABC. On note finalement M le milieu de BC.
Montrer que les points A_1,K,M et L sont cocycliques.

Mehdi.O a écrit:

Problème 23:
Soient x,y deux entiers naturels tel que xy|x²+y²-x.
Montrer que x est un carré parfait.

Tu peux lire une solution ici:
https://mathsmaroc.jeun.fr/t16497p465-preparations-aux-olympiades-de-premiere-2010-2011.
Merci de changer le problème courant.

Mehdi.O a écrit:

Voici un problème de géométrie assez facile mais délicieux à résoudre.
Problème 23:
Soit ABC un triangle dont les angles sont aigus. Le cercle inscrit de ABC touche BC,AC, et AB en D,E et F respectivement. La bissectrice de angle{BAC} coupe DE et DF en K et L respectivement. Et soit A_1 un point tel que AA_1 est une hauteur du triangle ABC. On note finalement M le milieu de BC.
Montrer que les points A_1,K,M et L sont cocycliques.

C'est bizarre, j'ai refait le schéma plusieurs fois, les points A_1,K,M et L ne sont pas cocycliques, pourriez-vous accompagner l'exercice avec une figure ?

ali-mes a écrit:

Mehdi.O a écrit:

Voici un problème de géométrie assez facile mais délicieux à résoudre.
Problème 23:
Soit ABC un triangle dont les angles sont aigus. Le cercle inscrit de ABC touche BC,AC, et AB en D,E et F respectivement. La bissectrice de angle{BAC} coupe DE et DF en K et L respectivement. Et soit A_1 un point tel que AA_1 est une hauteur du triangle ABC. On note finalement M le milieu de BC.
Montrer que les points A_1,K,M et L sont cocycliques.

C'est bizarre, j'ai refait le schéma plusieurs fois, les points A_1,K,M et L ne sont pas cocycliques, pourriez-vous accompagner l'exercice avec une figure ?

Tu as peut-être commis une erreur qualque part, voici la figure:

Spoiler:

Prends ton stylo maintenant :p !

lemme : ABC est un triangle ,C son cercle inscrit de centre I touche les cotés AC,BC,AB en E,D,F .P est l'intersection de (AI) et (BC) .(FD)et (AP) ce coupe en L , la droite (CL) coupe (AB) en N , on a L milieu de [NC]
Preuve:L'idée est de prouver que ILC=90 ainsi comme (AL) est un bissectrice et une hauteur L sera le milieu [NC] , pour prouver que ILC=90 , il suffit de prouver que ILCE est inscrit, prouvons cela .
il est remarquable que IDCE est inscrit puisque IDC+IEC=90+90=180 .
on veut prouver que ILDC l'est aussi,on a ICD+ILD=1/2ACB+180-ILF=1/2ACB+180-(180-1/2BAC-AFL)=1/2ACB+1/2BAC+AFD=1/2ACB+1/2ABC+180-DFB=1/2ACB+1/2BAC+180-[1/2(180-ABC)car DFB=BDF ainsi ICD+ILD=1/2ACB+1/2ABC+1/2BAC+90=180 ainsi IDCE est inscrit
on a IDCE et ILCE deux quadrilatère inscrit ainsi ILCE est aussi inscrit d'ou ILC=90 ainsi
L est le milieu de [NC]

Spoiler:

revenons a L'exo :
sois G l'intersection de (AB) et (CL)
d'aprés le lemme L est le milieu de [CG] , ainsi (LM)//(AB) d'ou
d'une autre part
On ainsi
d'une autre part :

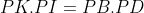prouvons que pour prouver cela il suffit de prouver que IBKA1 est inscrit
BDK=EDC=DEC---> 2BDK+ACB=180---> BDK=1/2(180-ACB)
BIK=180-BIA=180-(180-1/2ABC-1/2BAC)=180-180+1/2(ABC+ACB)=1/2(180-ACB)--> BIK=BDK
CQFD

Spoiler:

En attendant une confirmation voici
PROBLEMME 24:
c'est un peu banal mais c'est tous ce que j'ai trouvé pour le moment :
résoudre dans IN l'équation suivante :
x²+y²=3(z²+t²).

Solution au problème 24:
Il est bien clair d'après l'équation x²+y²=3(z²+t²) que 3|x²+y², ainsi en effectuant les congruences de x,y modulo 3 on trouve que x=0(mod 3) et y=0(mod 3), et ain si il existe deux entiers naturels k_1 et k_2 t.q= x=3k_1 et y=3k_2 ainsi on trouve z²+t²=3(k_1²+k_2²), en répétant le même processus avec z et t, on retrouve de nouveau que x et y sont congrus à 0 modulo 9 et ainsi de suite ... Ce logarithme nous permet de conclure que les valuations 3-adiques de x,y,z et t tendent vers l'infini, ce qui n'est vrai que lorsque les vairbales sont nuls. Et ainsi x=y=z=t=0.

Mehdi.O a écrit:

Solution au problème 24:
Il est bien clair d'après l'équation x²+y²=3(z²+t²) que 3|x²+y², ainsi en effectuant les congruences de x,y modulo 3 on trouve que x=0(mod 3) et y=0(mod 3), et ain si il existe deux entiers naturels k_1 et k_2 t.q= x=3k_1 et y=3k_2 ainsi on trouve z²+t²=3(k_1²+k_2²), en répétant le même processus avec z et t, on retrouve de nouveau que x et y sont congrus à 0 modulo 9 et ainsi de suite ... Ce logarithme nous permet de conclure que les valuations 3-adiques de x,y,z et t tendent vers l'infini, ce qui n'est vrai que lorsque les vairbales sont nuls. Et ainsi x=y=z=t=0.

Exacte,à toi !!

Sans perte de temps, je m'autorise de prendre le tour de Mehdi.O:
Problème 25:
Soit le cercle de centre 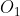et de rayon .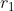
Et le cercle de centre 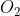et de rayon .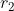
Les deux cercles et sont tangents extérieurement en un point qu'on note , on suppose de plus que .
Pour tout point de n'appartenant pas à , on considère le point de tel que le triangle soit rectangle en .
Démontrez que la droite passe par un point fixe.
Bonne chance.