Préparation aux olympiades.

Vos reponses sont justes ^^

aymanemaysae a écrit:

Pour offrir un moment de répit à tous les amis, et en guise de récréation voici un exercice que j'aime bien: Exo 30:

pour la deuxième je pense que la vraie question est de calculer :

il suffit de remarquer que :

alors :

Problème 31 :
Soient a, b et c trois nombres réels tels que , et .
On suppose qu'il existe des entiers naturels premiers entre eux tel que .
Calculez .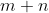
Bonne chance.

Bonjour Mlle Elmrini,
Pour l'exercice 31, voici ma proposition. J'espère qu'elle n'est pas fausse, même si je suis sûr que ce n'est pas la solution idéale.

Bonjour tout le monde;
Je ne vais pas proposer un exercice, mais c'est seulement un divertissement pour reposer nos méninges.

Vous êtes un champion M. Legend_Crush: j'avais une autre méthode qui etait essentiellement géométrique, mais votre approche est aussi élègante que concise.

Bravo.

A vous l'honneur de poster un exercice.

L-crush A vous de poster l'exercice 31

Exo 31:
resoudre en N², l'equation diophantienne, sachant que n est entier naturel, et p est premier:
n^3=p²-p-1

legend-crush a écrit:

Exo 31:
resoudre en N², l'equation diophantienne, sachant que n est entier naturel, et p est premier:

n^3=p²-p-1

pour : p=2 on trouve n=1

si p=3 alors n^3=7 impossible.

si p>5 alors pgcd(p,p-1)=1 et n^3=p²-p-1>5²-5-1=19 => n>3 => n^2-n+1>n+1

on a : n^2-n+1=(n+1)²-3n  et pgcd(n+1,n)=1 alors pgcd(n+1,n^2-n+1)=pgcd(n+1,3n)={1,3}

l'equation equivalente a : (n+1)(n^2-n+1)=p(p-1) et p>p-1

alors p|(n^2-n+1) => n^2-n+1=kp et p-1=k(n+1) avec k£{1,3}

si k=1 alors n^2-n+1=p et p-1=n+1 => n^2-n+1=n+2 => n^2-2n-1=0 impossible

si k=3 alors n^2-n+1=3p et p-1=3(n+1) => n^2-n+1=9(n+1)+3 => n^2-10n-11=0 => n=11 => p=37

les solutions : S(p,n)={(2,1);(37,11)}.

aymanemaysae a écrit:

pour la 2eme question :

n=a4b4 et p=b4a4 on a p>404>2 alors b>a

on a : avec 1<k<9

alors : 4k+2=4 mod(10)=> k={3,8}

si : k=3 donc 3b+1=a+10k' avec 0<k'<2 et b4a4=3*a4b4+2

*pour k'=0 on a : 3b+1=a et b>a impossible

*pour k'=1 on a : 3*4+1=4 mod(10) impossible

*pour k'=2 on a : 3*4+2=4 mod(10) vrai alors 3a+1=b et 3b+1=a+20 => a=2,b=7

si : k=8 donc 8b+3=a+10k' avec 0<k'<5 et b4a4=8*a4b4+2

*pour k'=0 on a : 8b+3=a et b>a impossible

*pour k'=1 on a : 8*4+1=4 mod(10) impossible

*pour k'=2 on a : 8*4+2=4 mod(10) vrai alors 8a+2=b et 8b+3=a+20 impossible dans N.

*pour k'=3 on a : 8*4+3=4 mod(10) impossible

*pour k'=4 on a : 8*4+4=4 mod(10) impossible

*pour k'=5 on a : 8*4+5=4 mod(10) impossible

la seul solution c'est : n=2474 et p=7424 on trouve : p=7424=3*2474+2=3n+2.

pour le 1 je vais essayer plus tard

Très bonne solution Mlle Lemrini, et pour preuve, voici la solution du livre .

elmrini a écrit:

legend-crush a écrit:

Exo 31:
resoudre en N², l'equation diophantienne, sachant que n est entier naturel, et p est premier:

n^3=p²-p-1

pour : p=2 on trouve n=1

si p=3 alors n^3=7 impossible.

si p>5 alors pgcd(p,p-1)=1 et n^3=p²-p-1>5²-5-1=19 => n>3 => n^2-n+1>n+1

on a : n^2-n+1=(n+1)²-3n  et pgcd(n+1,n)=1 alors pgcd(n+1,n^2-n+1)=pgcd(n+1,3n)={1,3}

l'equation equivalente a : (n+1)(n^2-n+1)=p(p-1) et p>p-1

alors p|(n^2-n+1) => n^2-n+1=kp et p-1=k(n+1) avec k£{1,3}

si k=1 alors n^2-n+1=p et p-1=n+1 => n^2-n+1=n+2 => n^2-2n-1=0 impossible

si k=3 alors n^2-n+1=3p et p-1=3(n+1) => n^2-n+1=9(n+1)+3 => n^2-10n-11=0 => n=11 => p=37

les solutions : S(p,n)={(2,1);(37,11)}.

Je n'ai pas bien compris comment on a passé de p>=5 a p^2-p-1 >= 5^2-5-1 psk si p>=5 donc -p=<-5 et non pas >=

bianco verde a écrit:

Je n'ai pas bien compris comment on a passé de p>=5 a p^2-p-1 >= 5^2-5-1 psk si  p>=5 donc -p=<-5 et non pas >=

la fonction f(x)=x²-x-1 est croissante pour tt x>1/2
on peut faire aussi : p^2-p-1 > 5^2-5-1 <=> p^2-5^2-p+5>0 <=> (p+4)(p-5)>0 qui est vrai

A vous de poster l ' exercice 32

bianco verde a écrit:

A vous de poster l ' exercice 32

j'attend une solution détaillée pour la deuxième question de Mr aymanemaysae car j'ai essayée, mais sans aucune résultat   .

Mr . aymanemaysae a précisé avant de poster son exo que ce dernier ne faisait pas de la partie , Donc vous pouvez poster votre exercice.
Amicalement.^_^

Pour l'exercice de factorisation, on peut remarquer que le polynôme se scinde en deux parties: 
x^8 + x + 1 et x^10 + x^5 + 1, puis pour chacun d'eux on utilise la méthode que j'ai apprise de votre exercice "Liiiimite", c-à-d soustraire puis ajouter.

1) x^8 + x + 1 = x^8 - x^7 + x^7 - x^6 + x^6 - x^5 + x^5 - x^4 + x^4 - x^3 + x^3 - x^2 + x^2 + x + 1
= (x^2 + x + 1)(x^6 - x^5 + x^3 - x^2 + 1) .
2)Pour x^10 + x^5 + 1 c'est la même chose, et on remarque que tous les deux sont des multiples de 
x^2 + x + 1, et le tour est joué.

bianco verde a écrit:

Mr . aymanemaysae a précisé avant de poster son exo que ce dernier ne faisait pas de la partie , Donc vous pouvez poster votre exercice.
Amicalement.^_^

bon je propose ce probleme :
On considère l'équation x²+mx+3m²-7m-19=0 où m est un paramètre réel .
Déterminer les valeurs de m pour lesquelles l'équation admet deux solutions x1 et x2 telles que :
1/(x1-2)+1/(x2-2)=-2m/13.

aymanemaysae a écrit:

Pour l'exercice de factorisation, on peut remarquer que le polynôme se scinde en deux parties: 
x^8 + x + 1 et x^10 + x^5 + 1, puis pour chacun d'eux on utilise la méthode que j'ai apprise de votre exercice "Liiiimite", c-à-d soustraire puis ajouter.

1) x^8 + x + 1 = x^8 - x^7 + x^7 - x^6 + x^6 - x^5 + x^5 - x^4 + x^4 - x^3 + x^3 - x^2 + x^2 + x + 1
= (x^2 + x + 1)(x^6 - x^5 + x^3 - x^2 + 1) .
2)Pour x^10 + x^5 + 1 c'est la même chose, et on remarque que tous les deux sont des multiples de 
x^2 + x + 1, et le tour est joué.

7ta wsselt bach ndiir l pgcd(x^10 + x^8 + 1,x^5 + x + 1) mai gelt robama maghate3ti walo pff   

c'est vrai que : "Beaucoup d'échecs de la vie sont vécues par les personnes qui ne se rendent pas compte à quel point ils étaient au succès quand ils ont abandonné."(Thomas Edison)

legend-crush a écrit:

Exo 33:

pourquoi pas :

Exercice 33.
Voici ma solution suivant la remarque de Mlle Elmrini.